[ QA ]
t통계량, t검정통계량, t검정통계값의 관계는?
CONTENTS
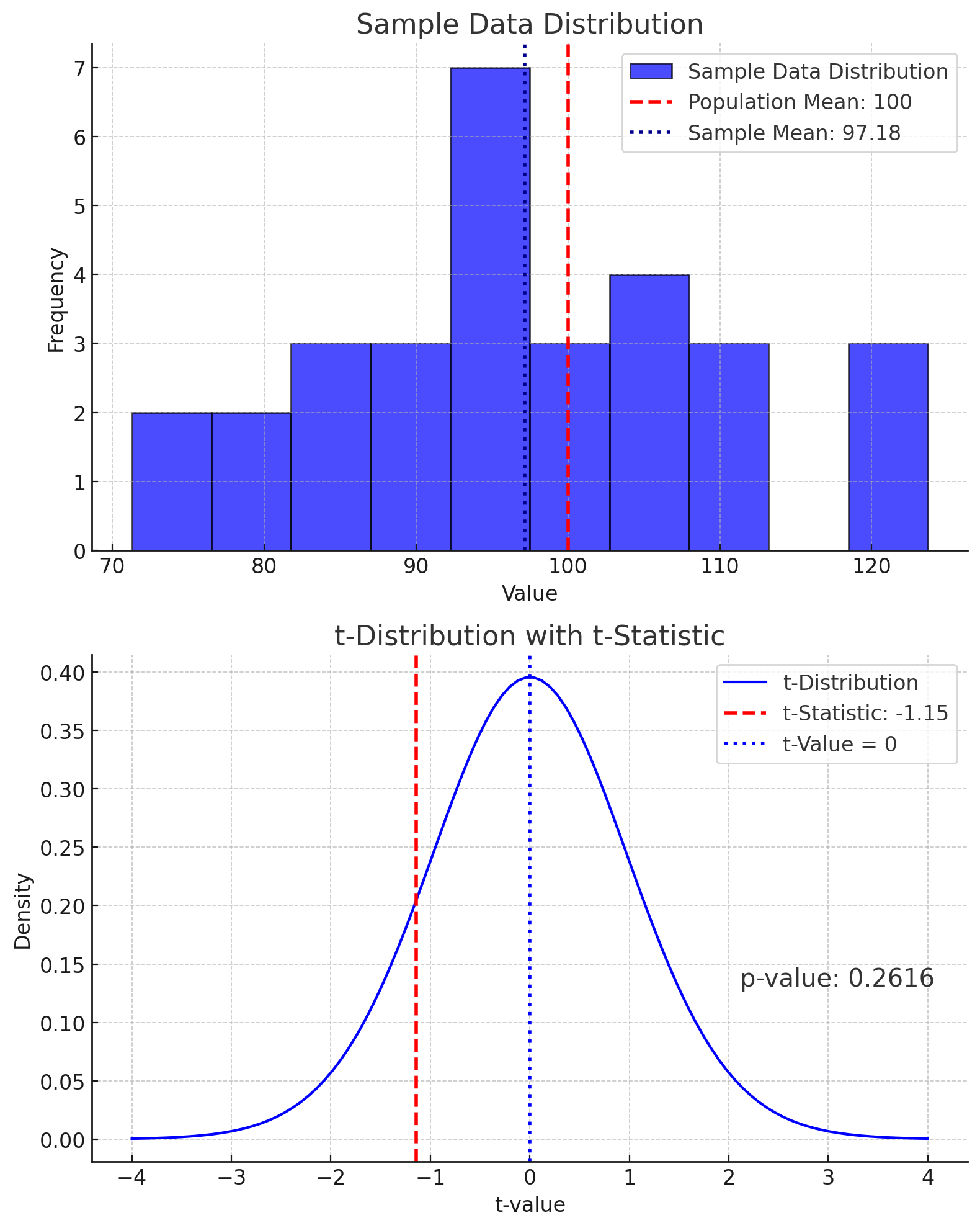
귀무가설을 통해 , t통계량의 변수의 수를 줄여 t검정통계량을 구합니다.
여기서, 귀무가설은 알 지 못하는 모수에 대한 가설입니다.
t검정통계량은 확률변수이며 정의된 확률분포함수로 표현합니다.
표본데이터를 통해, t검정통계량의 함수값인 t검정통계값을 구합니다.
t통계량, t검정통계량, t검정통계값의 관계
t통계량을 함수로 보면 다음과 같습니다.
$$t(\bar{X}, \mu, s, n) = \dfrac{\bar{X} – \mu}{\dfrac{s}{\sqrt{n}}}$$
여기서, $t$는 t통계량
$\nu$는 자유도: $\nu=n-1$
$n$은 표본크기
$\Gamma(\,\,\,)$는 감마함수
$\bar X$는 표본평균
$\mu$는 모평균
$s$는 표본표준편차
t통계량의 변수인 모평균, $\mu$가 귀무가설에 의해 $\mu_0$로 특정되어 t통계량은 t검정통계량이 됩니다.
$$\mu \rightarrow \mu_0$$
t검정통계량을 함수로 보면 다음과 같습니다.
$$t_{test}(\bar{X}, \mu_0, s, n) = \dfrac{\bar{X} – \mu_0}{\dfrac{s}{\sqrt{n}}}$$
여기서, $t_{test}$는 t통계량이며 t분포를 나타내는 확률변수: $t_{\text{test}}\rightarrow t$
$f(t ; \nu) = \frac{\Gamma\left(\frac{\nu + 1}{2}\right)}{\sqrt{\nu \pi} \ \Gamma\left(\frac{\nu}{2}\right)} \left(1 + \frac{t^2}{\nu}\right)^{-\frac{\nu + 1}{2}}$
$\nu$는 자유도: $\nu=n-1$
$n$은 표본크기
$\Gamma(\,\,\,)$는 감마함수
$\bar X$는 표본평균
$\mu_O$는 귀무가설로 가정된 모평균
$s$는 표본표준편차
표본데이터에서 표본평균과 표본표준편차와 표본크기가 관측되어 검정통계량의 함수값인 검정통계값을 구할 수 있습니다.
$$\bar X \rightarrow \bar X_{obs} = \frac{1}{n} \sum_{i=1}^{n} X_i$$
$$s \rightarrow s_{obs}=\sqrt{ \frac{1}{n-1} \sum_{i=1}^{n} (X_i – \bar{X})^2}$$
$$n \rightarrow n_{obs}$$
t통계량(t-statistic)
확률변수($X$)가 정규분포를 나타내면 표본평균($\bar X$)의 t통계량은 다음과 같습니다.
$$t = \dfrac{\bar{X} – \mu}{\dfrac{s}{\sqrt{n}}}$$
여기서, $t$는 t통계량
$\bar{X}$는 표본평균(sample mean)
$\mu$는 모평균(population mean)
$s$는 표본표준편차(population standard devitation)
$n$은 표본크기
$n-1$은 표본의 자유도: 표본내 개체의 자유도
t검정통계량(t-test statistic)
t검정의 사용예: 표본평균과 모평균의 비교
표본평균의 귀무가설에서의 t검정통계량은 다음과 같습니다.
$$t_{\text{test}} = \dfrac{\bar{X} – \mu_0}{\dfrac{s}{\sqrt{n}}}\sim t_{n-1}$$
여기서, $t_{\text{test}}$는 t검정통계량
$\bar{X}$는 관측된 표본평균(observed sample mean)
$\mu_0$는 귀무가설에서의 모평균(population mean under the null hypothesis)
$s$는 관측된 표본표준편차(observed sample standard devitation)
$n$은 표본크기
$(n-1)$은 표본의 자유도: 표본내 개체의 자유도
$t_{n-1}$은 자유도, (n-1)을 매개변수로 하는 t분포
t검정통계값(t-test statistic value)
t검정통계값 (t-test statistic value)은 다음과 같이 표현할 수 있습니다.
$$t_{\text{value}} = \dfrac{\bar{X}_{obs} – \mu_0}{\dfrac{s_{obs}}{\sqrt{n_{obs}}}}$$
여기서, $t_{\text{value}}$는 t검정통계값
${\bar X}_{obs}$는 관측된 표본평균:
${\bar X}_{obs} = \dfrac{1}{n} \sum\limits_{i=1}^{n} X_i$
$\mu_0$는 귀무가설에서 주장하는 모평균
$s_{obs}$는 관측된 표본표준편차:
$s_{obs} = \sqrt{\dfrac{1}{n-1} \sum\limits_{i=1}^{n} (X_i – \bar{X})^2}$
$n_{obs}$는 관측된 표본크기
t검정통계값은 t검정을 수행할 때 계산되는 값으로, 귀무가설과 표본 데이터 간의 차이를 측정하며 다음과 같은 역할을 합니다.
귀무가설과의 차이 측정: t검정통계값은 표본평균과 귀무가설에서 주장하는 모평균의 차이가 표본 데이터에서 얼마나 큰지를 수량화한 값입니다. 이 값을 통해 표본이 귀무가설에 의해 설명되는지, 아니면 대립가설을 고려해야 할지를 평가합니다.
p값 계산: t검정통계값을 이용하여 해당 값이 t분포에서 얼마나 극단적인지 확인한 후, 이를 바탕으로 p값을 계산합니다. p값은 귀무가설이 참일 때 t검정통계값처럼 극단적인 값이 나타날 확률을 의미합니다.
임계값과 비교: t검정통계값은 특정 유의수준(예: 0.05)에서 설정된 임계값과 비교하여, 귀무가설을 기각할지 여부를 결정하는 데 사용됩니다. t검정통계값이 임계값을 넘으면 귀무가설을 기각할 수 있습니다.
