연속형 확률변수가 유리수로 실현될 확률은?

연속형 확률변수가 유리수로 실현될 확률은 0입니다.

연속형 확률변수가 무리수로 실현될 확률은 1입니다.

실수의 확률공간

실수는 유리수와 무리수로 구성됩니다.

$$\mathbb{R} = \mathbb{Q} \cup (\mathbb{R} \setminus \mathbb{Q})$$

여기서, $\mathbb{R}$은 실수

$\mathbb{Q}$는 유리수

$(\mathbb{R} \setminus \mathbb{Q})$은 무리수: $\mathbb{R}$집합에서 $ \mathbb{Q}$집합을 뺀 집합

유리수와 무리수는 서로소(disjoint) 관계인 배타적인 집합입니다.

$$\mathbb{Q} \cap (\mathbb{R} \setminus \mathbb{Q}) = \emptyset$$

여기서, $\emptyset$은 원소가 없는 공집합

실수를 표본공간으로 하여 공집합, 유리수, 무리수, 실수를 원소로 하는 사건공간(시그마대수, $\sigma$-algebra)을 구성할 수 있습니다. 사건공간의 사건에 확률측도를 부여하여 확률공간을 표현할 수 있습니다.

$$\text{확률공간}: (\Omega, \mathcal{F}, P)$$

표본공간을 표현하면 다음과 같습니다.

$$\Omega=\mathbb{R}$$

사건공간을 표현하면 다음과 같습니다.

$$\mathcal{F}=\{\emptyset, \mathbb{Q}, \mathbb{R} \setminus \mathbb{Q}, \mathbb{R} \}$$

사건공간의 사건을 확률측도로 표현하면 다음과 같습니다.

$$P(\mathbb{R}) = P(\mathbb{Q}) + P(\mathbb{R} \setminus \mathbb{Q}) = 0 + 1 = 1$$

확률이론에 따라 정리하면, 표본공간인 실수($\mathbb{R}$)에서의 확률은 반드시 $1$ 이어야 합니다

$P(\text{실수}) = 1$

실수가 지지집합(support)인 연속형 확률변수에서 실수가 실현될 확률은 1입니다. 실수는 유리수와 무리수로 나뉘는데, 유리수가 실현될 확률이 $0$ 이므로 나머지 무리수에서의 확률은 $1$ 이어야 합니다

$P(\text{무리수}) = P(\text{실수}) – P(\text{유리수}) = 1 – 0 = 1$

연속형 확률변수가 유리수로 실현될 확률

유리수의 집합은 원소를 셀 수 있는 가산집합입니다. 그리고 갯수가 무한대인 무한집합입니다.

연속형 확률변수는 실수정의역 전체에 걸쳐 확률이 분포합니다. 그리고 개별 점이나 가산집합에서의 확률은 항상 0입니다.

유리수는 가산집합이므로, 개별 점의 확률이 0이고, 가산집합의 전체 확률도 입니다. 따라서, 유리수의 집합의 확률측도는 0입니다. 즉, 실수인 정의구역을 가지는 연속형 확률변수가 유리수로 실현될 확률은 없다고 봅니다.

연속형 확률변수에서는 확률밀도함수(PDF)를 사용해 구간의 확률을 계산합니다. 유리수는 연속된 실수 구간에서 점으로만 존재하므로, 그 점들이 차지하는 전체 확률은 0입니다.

측도론적 관점에서 유리수의 집합은 실수 집합에서 “0의 측도”를 가집니다. 즉, 유리수가 차지하는 공간의 크기가 0이기 때문에, 확률도 0으로 계산됩니다.

연속형 확률변수가 무리수로 실현될 확률

무리수의 집합은 원소를 셀 수 있는 가산집합이 아니며, 비가산집합입니다. 이는 무리수가 실수 집합의 “거의 모든 점”을 차지한다는 사실과도 일치합니다.

실수($\mathbb{R}$)는 비가산집합이고, 유리수($\mathbb{Q}$)는 가산집합이므로 실수집합에서 유리수집합을 뺸 무리수집합($\mathbb{R} \setminus \mathbb{Q}$)은 비가산집합입니다.

정리하면,

무리수는 실수에서 유리수를 제외한 부분집합입니다: $\mathbb{R} \setminus \mathbb{Q}$
실수($\mathbb{R}$)는 비가산집합입니다. 즉, 원소를 셀 수 없는 집합입니다.
유리수($\mathbb{Q}$)는 가산집합이므로, 실수에서 유리수를 제외한 나머지인 무리수는 여전히 비가산집합입니다.

가산집합과 비가산집합

가산집합(countable set)

가산집합(countable set)은 원소를 셀 수 있는 집합입니다. 원소의 개수가 유한인 유한집합(finite set)은 원소를 셀 수 있으므로 모든 유한집합은 가산집합입니다. 한편, 무한집합(infinite set)에서는 집합의 원소가 자연수와 일대일 대응을 이룰 수 있는 경우, 이 집합을 가산무한집합(countably infinite set)이라고 합니다. 가산무한집합의 예에는 자연수($\mathbb{N}$), 정수($\mathbb{Z}$), 유리수($\mathbb{Q}$)가 있습니다.
자연수는 그 자체로 자연수와 대응됩니다. 정수는 규칙을 가지고 자연수와 일대일 대응이 가능합니다. 유리수는 두 정수의 비율로 표현되므로 규칙을 가지고 자연수와 일대일 대응이 가능합니다.

비가산집합(uncountable set)

비가산집합(uncountable set)은 집합의 원소를 셀 수 없는 집합입니다. 그리고 비가산집합은 항상 무한집합(infinite set)입니다. 비가산집합의 원소와 자연수집합($\mathbb{N}$)의 원소는 일대일 대응이 불가능합니다. 비가산집합의 크기는 자연수집합이나 유리수집합의 크기보다 큽니다.

Table. 1. 가산집합과 비가산집합 비교

특징	가산집합	비가산집합
정의	자연수 집합 `ℕ`와 일대일 대응 가능.	자연수 집합 `ℕ`와 일대일 대응 불가능.
원소의 개수	유한집합 또는 가산무한집합 (`ℵ₀`)	무한집합 (`2^ℵ₀` 이상)
원소를 셀 수 있나?	셀 수 있음	셀 수 없음
대표적 예	자연수 집합 `ℕ` 정수 집합 `ℤ` 유리수 집합 `ℚ`	실수 집합 `ℝ` 구간 [0, 1] 무리수 집합 $\mathbb{R}\setminus\mathbb{Q}$
크기 (기수)	`ℵ₀` (가산 무한 크기)	`2^ℵ₀` (비가산 무한 크기)
부분집합 관계	모든 유한집합은 가산집합에 포함됨	비가산집합은 가산집합보다 더 큰 집합임
생성 방식	유한 개의 선택 + 가산 합집합	칸토어의 대각선 논법으로 비가산성 증명 가능
적용 사례	데이터, 알고리즘에서 순서나 나열 가능한 데이터	연속 데이터나 함수공간에서의 분석

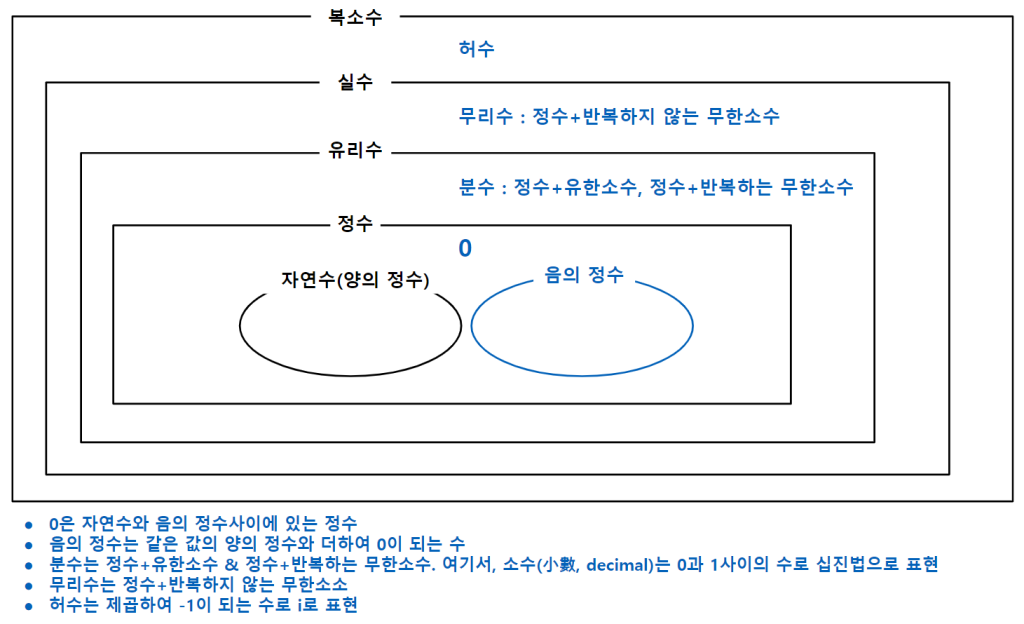
Fig. 1. 수체계

Q-data : 2

Q&A : 23

Quiz : 180

0000-0000