자연상수 e(약 2.71828…)입니다.
지수함수에서 밑을 아무 번도 곱하진 않은, 즉 지수가 0인 지수함수의 함수값은 항상 1입니다.
$$a^0=1$$
여기서, $a$는 양의 실수
지수가 0인 지점에서 함수값처럼 변화율(기울기)마저 정확히 1이 되는 특별한 밑이 자연상수 e입니다.
$$e^0 = 1 \quad (\text{함수값}), \quad \left. \frac{d}{dx}e^x \right|_{x=0} = 1 \quad (\text{기울기})$$
여기서, $\left.\frac{d}{dx}e^x \right|_{x=0} =\left.\lim\limits_{\Delta x \to 0} \frac{e^x( e^{\Delta x} – 1)}{\Delta x}\right|_{x=0}=\lim\limits_{\Delta x \to 0} \frac{ e^{\Delta x} – 1}{\Delta x} = 1$
주기율($\pi$)이 회전과 병진의 관계를 설명한다면, 자연상수($e$)는 생성(소멸)과 변환(진화)의 관계를 설명합니다.
황금비($\phi$)는 자기유사성과 형성의 관계를 설명합니다.
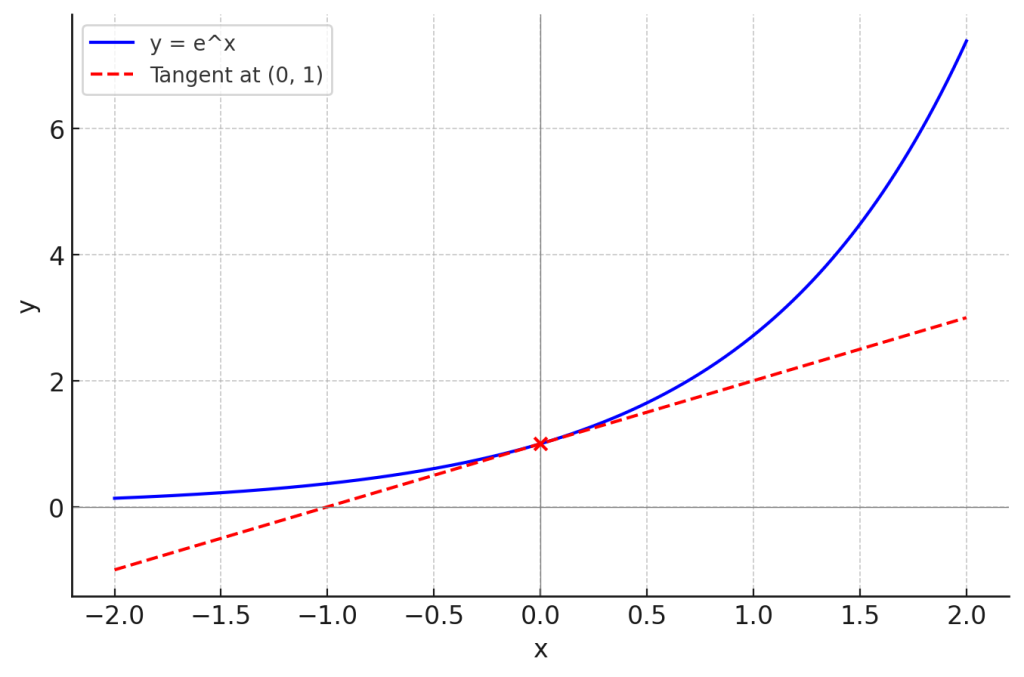
Fig.1 지수가 0일 때, 변화율이 1이 되는 지수함수: $y=e^x$
지수함수에서 밑을 아무 번도 곱하진 않은, 즉 지수가 0인 지수함수의 함수값은 항상 1입니다.
$$a^0=1$$
여기서, $a$는 양의 실수
지수가 0인 지점에서 순간변화율(기울기)마저 정확히 1이 되는 특별한 밑이 자연상수 e입니다.
$$e^0 = 1 \quad (\text{함수값}), \quad \left. \frac{d}{dx} e^x \right|_{x=0} = 1 \quad (\text{기울기})$$
여기서, $\frac{d}{dx} e^x =\lim_{\Delta x \to 0} \frac{e^{\Delta x} – 1}{\Delta x} = 1$
지수가 0일 때 순간변화율은 다음식으로 표현합니다.
$$\left. \frac{d}{dx} e^x \right|_{x=0} =\lim_{\Delta x \to 0} \frac{e^{0+\Delta x} – e^0}{\Delta x}=\lim_{\Delta x \to 0} \frac{e^0(e^{\Delta x} – 1)}{\Delta x} =\lim_{\Delta x \to 0} \frac{e^{\Delta x} – 1}{\Delta x} = 1$$
여기서, $e^0=1$
$e^{\Delta x}$는 지수함수로 x=0 근처에서의 함수값을 표현합니다. $e^x$라는 함수가 x=0 지점에서의 기울기(순간변화율, 미분값)가 정확히 1임을 의미합니다.
자연상수 $e$로 만든 지수함수 $e^x$는 x=0 위치에서 함수값이 정확히 1이면서 기울기(순간변화율)도 정확히 1인 유일한 함수입니다. 이러한 특징을 만족하는 숫자가 바로 자연상수 $e \approx 2.71828$ 입니다.
이식을 더 간단히 바꾸어 보면
$$e^{\Delta x} \approx 1+ \Delta x$$
매우 작은 구간 $\Delta x$에서 함수 $e^x$는 현재 값 1에서 구간 크기 $\Delta x$만큼 비례하여 증가한다는 뜻입니다.
예를 들어 구간이 아주 작은 $\Delta x=0.001$일 때 $e^0.001 \approx 1+0.001$ 처럼 높이가 약간 커지는 데 기울기(증가량)가 정확히 그 구간 길이만큼 증가한다는 뜻입니다. 이러한 미세한 성질을 계속 반복하면, 결국 무한히 잘게 나눠진 증가가 누적되면서, 자연상수 $e\approx 2.71828$라는 값으로 수렴합니다.
자연상수 $e$는 지수함수 $e^x$의 값과 가울기가 $x=0$에서 동시에 1이 되도록 만드는 유일한 숫자입니다. 자연상수 $e$는 실수 중에서 무리수입니다.
내가 서 있는 높이와 그 지점에서의 경사면의 기울기가 항상 같게 되는 어떤 경사면이 있습니다.
높이 1m에서 시작하고 같은 속도로 평행 이동하면 경사는 점점 급경사를 나타냅니다. 왜냐하면 이동하면서 동시에 오르기 떄문입니다.
높이 1m에서 시작한다면 기울기가 1입니다. 45도 경사면입니다.
이 상태에서 1m/s 속도로 이동하면 자연적으로 $t$초가 지나면 $e^t $ m만큼 올라가게 됩니다.
중요한 것은 1초가 지났을 때 높이가 $e \approx 2.718\ldots$로 수렴한다는 것입니다.
그렇다면, $x$초가 지났을 때 높이를 정확히 $e^x$라고 표현할 수 있습니다.
특수 경사면에 르베그적분을 적용하면 “높이(함수값)”를 먼저 나누고, 각 높이에 해당하는 시간(측도)을 고려합니다.
이를 직관적으로 생각하면:
– 높이가 1 → 기울기 1 → 시간 Δt 동안 $e^1$로 성장
– 높이가 $e$ → 기울기 $e$ → 같은 시간 동안 $e^2$으로 성장
– 높이가 $e^x$ → 기울기 $e^x$ → 같은 시간 동안 $e^{x+\Delta x}로 성장
즉, 높이별로 측정한 기울기(미분값)를 기반으로 적분하는 방식이 르베그 적분의 접근 방식과 유사합니다.
이를 르베그적분으로 표현하면, 즉, 측도 공간에서 함수값을 기준으로 적분하면 다음식과 같습니다.
$$\int_{1}^{e^x} \dfrac{dy}{y} =x$$
위 적분식은 본질적으로 르베그적분에서의 로그적 성질을 활용한 것입니다.
특수 경사면은 높이와 기울기가 항상 같은 지수 성장 모델을 설명하는데, 이를 르베그 적분과 연결하면
– 리만 적분에서는 “시간 구간에 따른 누적 높이 변화”로 계산
– 르베그 적분에서는 “특정 높이에 대해 그 높이의 기울기를 측정하는 방식”으로 접근
결과적으로 르베그적분을 사용하면 지수적 성장을 로그 적분을 통해 더 자연스럽게 해석할 수 있게 됩니다.
시간 변화에 대한 측정을 바탕으로 적분을 수행하지 않고 “높이 변화에 대한 측정”을 바탕으로 적분을 수행하는 것이 르베그적분과의 핵심적 연결점입니다.
아래 현상은 자연상수 $e$가 지수함수에서 “현재 값과 변화속도가 항상 동일한 유일한 밑$이기 때문에 발생하는 결과입니다.
자연상수 $e$가 밑인 지수함수 $e^x$를 0에서 1까지 적분하면 정확히 $(e-1)$이 됩니다. 이는 적분(넓이)으로 표현했을 때, 0에서 1까지의 면적이 정확히 $(e-1)$이라는 명확한 값을 가짐을 의미합니다.
\[
\int_0^1 e^x dx = e – 1 \approx 1.71828
\]
자연상수 $e$는 지수가 1만큼 증가할 때 정확히 자기 자신의 배수로 증가하는 성질을 갖고 있습니다. 즉, 지수가 0에서 1로 증가하면 함수값이 정확히 약 2.71828배로 증가합니다.
\[
e^0 = 1, \quad e^1 = e \approx 2.71828
\]
함수 $e^x$는 언제, 어느 지점에서 보더라도 변화율(기울기)이 정확히 그 지점에서의 함수값과 같습니다. 예를 들어, $x=2$에서의 함수값과 미분값이 모두 동일하게 $e^2 \approx 7.3819$입니다. 즉, “함수값=순간 변화율”의 관계가 항상 성립하는 특별한 함수입니다.
\[
\frac{d}{dx} e^x = e^x
\]
숫자 1에서 시작하여 아주 작은 수 $\frac{1}{n}$만큼을 무한히 곱해 나가면 정확히 자연상수 $e$로 수렴합니다. 즉, 연속해서 아주 작은 증가를 무한히 반복하면 자연스럽게 $e \approx 2.71828$로 향하는 현상이 발생합니다.
\[
\lim_{n \to \infty} \left( 1 + \frac{1}{n} \right)^n = e
\]
함수 $e^x$는 미분과 적분을 무한히 반복해도 형태가 바뀌지 않는 특별한 함수입니다. 미분해도 원래 함수 그대로 남고, 적분해도 $C$를 제외하면 원래 함수 그대로 유지됩니다.
\[
\frac{d}{dx} e^x = e^x
\]
\[
\int e^x dx = e^x + C
\]
무한히 작은 증가량이 무한히 많아 질 때, 최종적ㅇ로 $e$라는 특정한 값에 수렴합니다. 수렴하는 숫자는 연속적인 성장의 극한인 한계값을 의미합니다. 이를 수식으로 나타내면 다음과 같습니다.
$$e=\lim_{n \to \infty}\left(1+\dfrac{1}{n}\right)$$
지수함수 \( e^x \)를 무한급수(infinite series)인 테일러급수로 전개하면 다음과 같습니다.
\[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \dfrac{x^n}{n!}\]
$x = 1$이면 지수함수의 값은 $e$입니다.
\[ e^1 = 1 + 1 + \frac{1^2}{2!} + \frac{1^3}{3!} + \cdots = \sum_{n=0}^{\infty} \dfrac{1^n}{n!}=\sum_{n=0}^{\infty}\dfrac{1}{n!}\]
지수함수 \( e^x \)를 무한급수(infinite series)인 테일러급수로 전개하면 다음과 같습니다.
\[ e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots = \sum_{n=0}^{\infty} \dfrac{x^n}{n!}\]
$( x = 0 )$ 근처에서 극한을 살펴보기 위하여 극한식을 다시 써보면 다음과 같습니다.
\[ \frac{e^{\Delta x} – 1}{\Delta x} = \frac{\left(1 + \Delta x + \frac{\Delta x^2}{2!} + \frac{\Delta x^3}{3!} + \cdots\right) – 1}{\Delta x} \]
분자에서 1이 소거되므로,
\[ = \frac{\Delta x + \frac{\Delta x^2}{2!} + \frac{\Delta x^3}{3!} + \cdots}{\Delta x} \]
여기서 $( \Delta x )$로 약분하면,
\[ = 1 + \frac{\Delta x}{2!} + \frac{\Delta x^2}{3!} + \frac{\Delta x^3}{4!} + \cdots \]
이제 $( \Delta x \to 0 )$으로 극한을 취하면, 나머지 항들은 모두 $( \Delta x )$를 포함하기 때문에 0으로 사라지고, 오직 1만 남게 됩니다. 따라서 다음식이 증명됩니다.
\[ \lim_{\Delta x\to 0} \frac{e^{\Delta x} – 1}{\Delta x} = 1 \]
따라서 $x=0$에서의 $e^x$의 변화율은 1입니다.