Menu
Menu
DATA ARTICLE : 2
LEARNING ARTICLE : 4
6 Weeks in Review
2 Weeks in Publication
Open Access
Peer Reviewed
eISSN 0000-0000
Menu
데이터사이언스 분야는 빠르게 발전하고 있으며, 고품질 데이터셋에 대한 접근은 학습과 연구에 필수적이다. 그러나 실제 데이터를 수집하는 과정은 비용이 많이 들고 접근이 어렵다. 이러한 문제를 해결하고, 효과적인 데이터사이언스 교육을 위한 합성 데이터셋을 생성하였다. 이 데이터셋은 딸기의 상품 가치를 나타내며, 비용 효율적이고 접근이 용이할 뿐만 아니라 개인정보 보호의 부담도 없다.
이 데이터셋은 두 가지 가상 품종의 딸기 출하월, 당도, 과중 데이터를 제공한다. 학습자는 이 데이터셋을 통해 다양한 통계적 분석 방법을 실습할 수 있으며, 통계적 사고 능력을 향상시킬 수 있다. 구체적으로는, 대응표본 t검정, 독립표본 t검정, 일원분산분석 F검정, 상관분석 t검정, 단순선형회귀분석 F검정, 교차분석 카이제곱검정 등을 이해하고 유의확률을 구하는 데 사용할 수 있다.
생성된 데이터는 Google Sheets를 사용하여 별도의 프로그램 설치 없이 인터넷 접속만으로 어디서든 열람이 가능하다. 가상의 딸기 품종 ‘설’과 ‘아키’를 각각 12월부터 4월까지의 출하월에 총 10,000개의 데이터를 생성하였으며, 출하월별 딸기의 성숙일 수, 당도, 과중, 숙성 후 당도 데이터를 포함한다. 출하월의 기후에 따라 성숙일 수가 달라지며, 성숙일 수에 따라 당도와 과중이 결정된다. 따라서, 당도와 과중 데이터를 분석함으로써 어느 시기에 딸기의 상품가치가 가장 높은지에 대한 직관을 가질 수 있도록 하였다.
이 연구는 고품질 데이터에 대한 접근을 용이하게 하여 데이터사이언스 교육과 연구를 촉진시키고, 제한된 자원을 가진 학습자들에게도 포괄적이고 효과적인 학습 경험을 제공한다. 생성된 데이터셋의 통계량과 모델식은 Google Sheets를 통해 접근 가능하다.
상품가치의 관점에서 딸기의 상품가치를 평가하는 속성을 관심있는 결과변수로 하여, 그 결과변수의 원인이 되는 변수를 찾는 능력을 배양하기 위한 실습 루틴을 개발하는 프로젝트의 모집단 생성 모델[1]에 따라 가상 딸기 데이터셋을 생성하였다.
데이터사이언스 분야는 빠르게 진화하고 있으며, 효과적인 학습과 연구를 위해 고품질의 데이터셋 접근이 필수적이다. 그러나 실제 데이터를 수집하는 과정은 비용과 접근성 측면에서 여러 가지 어려움에 직면하게 된다. 데이터 획득, 처리 및 유지보수와 관련된 상당한 경제적 투자가 필요하며, 이는 교육 기관, 소규모 연구팀 및 개인 학습자에게 금전적인 장벽을 만들어 진입을 제한하고 실습 기회를 제한하게 된다[2,3].
더욱이, 데이터사이언스 교육과 연구를 위해 실제 데이터셋을 사용할 때는 몇 가지 한계가 동반된다. 실제 데이터는 측정 오차가 클 수 있으며, 학습 목표를 달성하기에 일관성이 결여된 경우가 많아 초보 학습자들의 학습 과정을 복잡하게 만든다[4]. 또한, 개인정보 보호 문제와 규제 제한으로 인해 민감한 정보를 포함한 특정 데이터셋의 가용성과 사용이 더욱 제한될 수 있다. 이러한 요인들은 데이터사이언스 기술의 실질적인 적용과 분석 능력 개발을 저해한다.
이러한 문제를 해결하기 위해, 데이터사이언스 교육을 위해 특별히 설계된 합성 데이터셋을 생성할 수 있다. 우리의 데이터셋은 정규 분포를 사용하여 생성된 딸기 상품 가치이다. 확률분포를 이용하여 실제 데이터를 시뮬레이션함으로써 복잡성과 변동성을 유지하면서도 비용 효율적이고 쉽게 접근할 수 있는 자원을 제공할 수 있다[5].
이 접근법은 실제 데이터 수집과 관련된 경제적 장애물과 수집 과정에서의 어려움을 극복할 뿐만 아니라, 통제되고 맞춤화된 학습 환경을 보장한다. 학습자들은 실제 데이터셋에 내재된 잡음과 불규칙성에서 벗어나 기본 개념과 기술을 습득하는 데 집중할 수 있다. 또한, 합성 데이터셋의 특성상 개인정보 보호 문제가 없어 교육 목적으로 자유롭게 사용할 수 있다.
소비자들은 과일 선택 시 맛, 특히 당도를 가장 중요한 기준으로 여긴다[6]. 이 데이터셋은 상품가치와 직결되는 당도 데이터의 비교 및 이와 관련된 데이터와의 관계를 보여줄 수 있도록 생성되었다. 또한 하나의 데이터셋으로 대응표본 t검정, 독립표본 t검정, 일원분산분석 F검정, 상관분석 t검정, 단순선형회귀분석 F검정, 교차분석 카이제곱검정을 이해해서 유의확률을 구할 수 있도록 하여, 정규분포, t분포, F분포, 카이제곱분포에 대한 이해와 직관을 키우는 것을 목적으로 하였다. 이는 통계적 분석 방법과 확률 분포의 중요성을 이해하고, 다양한 분석 기술을 실습하여 통계적 사고 능력을 향상시키는 데 큰 도움이 될 것이다[7,8].
재배환경에 따라 달라지지만, 우리나라에서 소비되고 있는 딸기는 주로 10-11월 사이에 개화하고, 개화 후 25-40일 사이에 수확하며, 수확기간은 12월부터 4월까지이다[9]. 딸기는 더 서늘한 기후에서 천천히 자라면서 당분을 많이 축적하는데, 우리나라의 겨울철 딸기는 봄철 딸기에 비해 당도가 더 높고, 과육이 단단하다[10,11]. 이 논문에서는 딸기의 이러한 특성을 반영하되, 효과적인 데이터 사이언스 교육 효과에 보다 집중하여 가상의 딸기 품종과 데이터를 생성하였다. 이 가상의 딸기들은 개화부터 수확까지의 성숙일이 12월부터 4월까지 줄어들고, 이 성숙일이 원인이 되어 당도와 과중에 영향을 준다. 따라서, 당도를 분석함으로써 소비자에게 친화적인 딸기의 제철에 대한 직관을 가질 수 있을 것이다.
이 생성 데이터셋에서는 2가지 가상 딸기 품종의 출하월, 과중, 저온숙성 전후 당도 데이터를 제공한다.
본 연구에서 생성한 딸기 상품 가치 데이터셋은 데이터 접근성과 비용 측면에서의 문제를 해결하고, 고품질 데이터에 대한 접근의 어려움을 없애서 제한된 자원을 가지고 있는 데이터사이언스 지망생들에게도 포괄적이고 효과적인 학습 경험을 제공한다.
데이터셋의 생성은 사용자의 편의를 고려하여 브라우저와 인터넷 접속이 가능하다면, 별도의 프로그램 설치가 필요없고, 어디에서든 사용이 가능한 Google Sheets (Google LLC, USA)를 사용하였다.
가상의 딸기 품종 ‘설(Seol)’과 ‘아키(Aki)’를 12월부터 다음 해 4월까지, 5개월 동안 수확하는 것으로 하여 품종별 5,000개씩, 총 10,000개의 딸기 데이터를 생성하였다. 각 출하월에 수확한 딸기의 딸기꽃 개화부터 수확까지의 성숙일 수를 당도와 과중에 영향을 주는 변수로 하였다.
가상 딸기는 겨울이 제철인 딸기인데, 그 이유는 서늘한 기온에서 상대적으로 오랫동안 성숙되어 당도가 더욱 축적되고, 식감도 좋아진다. 이 딸기들의 성숙일 수는 12월부터 4월까지 평균이 36일, 표준편차가 2일인 정규분포를 따른다. 이를 이산형 데이터로 근사하여 12월부터 4월까지 각각 40, 38, 36, 34, 32일로 하였다.
설의 당도는 각 출하월의 당도 평균과 표준편차가 0.25인 정규분포를 이룬다. 각 출하월의 당도 평균은 성숙일 수에 0.3을 곱한 값이다. 이는 성숙일 수에 0.3을 곱하고, 평균이 0, 표준편차가 0.25인 정규분포를 이룬 오차를 더한 것으로 이해할 수 있다. 이 오차는 성숙일의 분포로부터 독립적이다.
설의 과중은 각 출하월의 과중 평균과 표준편차가 0.25인 정규분포를 이룬다. 각 출하월의 과중 평균은 성숙일 수에 0.6을 곱한 값이다. 이 또한 성숙일 수에 0.6을 곱하고, 평균이 0, 표준편차가 0.25인 정규분포를 이루는 오차를 더한 것과 결과적으로 동일한 분포이다. 이 오차는 성숙일의 분포로부터 독립적이다.
아키의 당도는 각 출하월의 당도 평균과 표준편차가 0.5인 정규분포를 이룬다. 각 출하월의 당도 평균은 성숙일 수에 0.25를 곱한 값이다. 이는 성숙일 수에 0.25를 곱하고, 평균이 0, 표준편차가 0.5인 정규분포를 이룬 오차를 더한 것으로 이해할 수 있다. 이 오차는 성숙일의 분포로부터 독립적이다.
아키의 과중은 각 출하월의 과중 평균과 표준편차가 0.25인 정규분포를 이룬다. 각 출하월의 과중 평균은 성숙일 수에 0.5를 곱한 값이다. 이 또한 성숙일 수에 0.5를 곱하고, 평균이 0, 표준편차가 0.25인 정규분포를 이루는 오차를 더한 것과 결과적으로 동일한 분포이다. 이 오차는 성숙일의 분포로부터 독립적이다.
설의 숙성 후 당도는 설의 기존 당도에 0.2를 더하고, 평균이 0, 표준편차가 0.1인 정규분포를 더하였다. 아키의 숙성 후 당도는 아키의 기존 당도에 0.1을 더하고, 평균이 0, 표준편차가 0.1인 정규분포를 더하였다. 이 각각의 정규분포는 기존 당도 분포로부터 독립적이다.
데이터 생성에 사용한 모델과 매개변수(parameter)는 Table 1에 정리하였다.
Table 1. Model and parameters of the strawberry synthetic data
| Variable | Generative model | Parameters of cultivar ($^1 x$) | |
|---|---|---|---|
| Seol | Aki | ||
| 성숙일 $(^2x)$ | $$^2X \sim N(\mu_{^2X}, \sigma_{^2X}^2) $$
여기서, $^2X$는 성숙일: 성숙일은 0과 양의 실수 $\mu_{^2X}$는 성숙일의 모평균 $\sigma_{^2X}^2$은 성숙일의 모분산 $^2X_i$, $i$는 출하연속월수 출하연속월수는 각각 1=12월, 2=다음해 1월, 3=다음해 2월, 4=다음해 3월, 5=다음해 4월 |
${^2X} \sim N(36, 2^2)$ 위의 정규분포를 5개의 구간으로 나누어 각 구간의 누적확률밀도로 수준(level)의 크기를 정하고 각 구간의 중앙값을 수준(level)의 값으로 정함. $P({^2X} = {^2x_i}) = \begin{cases} P(X \leq -1.5) = \displaystyle \int_{-\infty}^{-1.5} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \approx 0.0668 & \text{if } {^2x_1} = 40 \\ P(-1.5 \leq X \leq -0.5) = \displaystyle \int_{-1.5}^{-0.5} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \approx 0.2417 & \text{if } {^2x_2} = 38 \\ P(-0.5 \leq X \leq 0.5) = \displaystyle \int_{-0.5}^{0.5} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \approx 0.3829 & \text{if } {^2x_3} = 36 \\ P(0.5 \leq X \leq 1.5) = \displaystyle \int_{0.5}^{1.5} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \approx 0.2417 & \text{if } {^2x_4} = 34 \\ P(1.5 \leq X) = \displaystyle \int_{1.5}^{\infty} \frac{1}{\sqrt{2\pi}} e^{-\frac{x^2}{2}} \, dx \approx 0.0668 & \text{if } {^2x_5} = 32 \\ \end{cases}$ | |
| 저온숙성 $(^3x)$ | $${^1y}_{2}={^1y}_{1}+\bar{D}+\epsilon_{D}$$
여기서, ${^1y}_{2}$는 저온숙성 후 개체의 당도 ${^1y}_{1}$은 저온숙성 전 개체의 당도 $D$는 저온숙성 전후 당도차이이며 확률변수: $d={^1y}_{2}-{^1y}_{1}$, $D=\bar{D}+\epsilon_{D}$ $\bar{D}$는 저온숙성으로 인한 당도변화의 평균 $\epsilon_{D}$는 오차항이며 평균이 0이고 분산이 $\sigma_{D}^2$인 정규분포를 나타냄: $\epsilon_{D} \sim N(0, \sigma_{D}^2) $ |
$\bar{_1D}=0.20$ $\epsilon_{_1D} \sim N(0, \sigma_{_1D}^2) $ $\sigma_{_1D}^2=0.10^2$ | $\bar{_2D}=0.10$ $\epsilon_{_2D} \sim N(0, \sigma_{_2D}^2) $ $\sigma_{_2D}^2=0.10^2$ |
| 당도 $(^1y)$ | $$^1y=\beta_{0,^1Y}+\beta_{1,^1Y}{\cdot} {^2x}+\epsilon_{^1Y}$$
여기서, $^1y$는 당도 $\beta_{0,^1Y}$는 성숙일에 대한 당도의 회귀직선의 절편이며 값이 0 $\beta_{1, ^1Y}$는 성일에 대한 당도의 회귀직선의 기울기 $\epsilon_{^1Y}$은 오차항이며 평균이 0이고 분산이 $\sigma_{^1Y}^2$인 정규분포: $\epsilon_{^1Y} \sim N(0, \sigma_{^1Y}^2)$ |
$\beta_{1, {_1^1Y}}=0.30$ $\epsilon_{_1^1Y} \sim N(0, \sigma_{_1^1Y})$ $\sigma_{_1^1Y}^2=0.25^2$ | $\beta_{1, {_2^1Y}}=0.25$ $\epsilon_{_2^1Y} \sim N(0, \sigma_{_2^1Y})$ $\sigma_{_2^1Y}^2=0.50^2$ |
| 과중 $(^2y)$ | $$^2y=\beta_{0,^2Y}+\beta_{1,^2Y}{\cdot} {^2x}+\epsilon_{^2Y}$$
여기서, $^2y$는 과중 $\beta_{0,^2Y}$는 성숙일에 대한 과중의 회귀직선의 절편이며 값이 0 $\beta_{1, ^2Y}$는 성숙일에 대한 과중의 회귀직선의 기울기 $\epsilon_{^2Y}$은 오차항이며 평균이 0이고 분산이 $\sigma_{^2Y}^2$인 정규분포: $\epsilon_{^2Y} \sim N(0, \sigma_{^2Y}^2)$ |
$\beta_{1, {_1^2Y}}=0.60$ $\epsilon_{_1^2Y} \sim N(0, \sigma_{_1^2Y})$ $\sigma_{_1^2Y}^2=0.25^2$ | $\beta_{1, {_2^2Y}}=0.50$ $\epsilon_{_2^2Y} \sim N(0, \sigma_{_2^2Y})$ $\sigma_{_2^2Y}^2=0.25^2$ |
이렇게 생성된 설과 아키의 당도, 과중, 저온숙성 후 당도는 각각의 평균과 표준편차를 가지는 정규분포를 이룬다(Table 2).
Table 2. Distribution and parameters of the strawberry synthetic data
| Cultivar | Distribution | Sweetness (Brix) | Weight (g) | Sweetness after cold aging (Brix) |
|---|---|---|---|---|
| Seol | Normal | 10.80 ± 0.65 | 21.60 ± 1.24 | 11.00 ± 0.66 |
| Aki | Normal | 9.00 ± 0.71 | 18.00 ± 1.04 | 9.10 ± 0.72 |
Mean ± standard deviation.
The standard deviation has been rounded to the second decimal place.
앞의 모델에 따라 각 5,000개씩의 설과 아키의 당도, 과중, 숙성 후 당도 데이터를 생성하였고, 이의 통계량은 Table 3과 같다.
Table 3. Descriptive statistics of the strawberry synthetic data
| Cultivar | N | Sweetness (Brix) | Weight (g) | Sweetness after cold aging (Brix) |
|---|---|---|---|---|
| Seol | 5,000 | 10.80 ± 0.66 | 21.59 ± 1.24 | 11.00 ± 0.66 |
| Aki | 5,000 | 9.00 ± 0.71 | 17.99 ± 1.03 | 9.10 ± 0.72 |
Mean ± standard deviation.
The mean has been rounded to the second decimal place and the standard deviation has been rounded to the second decimal place.
정규분포 ${^2X} \sim N(36, 2^2)$를 5개의 구간으로 나누어 각 구간의 누적확률밀도로 수준의 크기를 정하고, 각 구간의 중앙값을 수준의 값으로 정하였다. 설과 아키의 과중과 당도는 이 수준의 값, 즉 성숙일에 기울기를 곱하고 오차를 추가하여 선형관계를 가지도록 하였다. 숙성 후 당도는 당도에 두 품종 각각의 차이를 더하고 오차를 추가하였다. 각 데이터 생성은 Google Sheets (Google LLC, USA)가 제공하는 함수를 사용하였다(Table 4).
Table 4. Data generation procedure and functions
| Variable | Procedure | Function | |
|---|---|---|---|
| Seol | Aki | ||
| 성숙일 $(^2x)$ | ${^2X} \sim N(36, 2^2)$ 위의 정규분포를 5개의 구간으로 나누어 각 구간의 누적확률밀도로 수준(level)의 크기를 정하고 각 구간의 중앙값을 수준(level)의 값, 즉 성숙일로 정함. | 첫번째 구간의 누적확률밀도 = NORMSDIST(–1.5)-NORMSDIST(–9.99999E+307) 두번째 구간의 누적확률밀도 = NORMSDIST(-0.5)-NORMSDIST(-1.5) 세번째 구간의 누적확률밀도 = NORMSDIST(0.5)-NORMSDIST(-0.5) 네번째 구간의 누적확률밀도 = NORMSDIST(1.5)-NORMSDIST(0.5) 다섯번째 구간의 누적확률밀도 = NORMSDIST(9.99999E+307)-NORMSDIST(1.5) | |
| 저온숙성 $(^3x)$ | 모델에 따라 저온숙성 당도 차이를 더하고 오차를 추가하여 저온숙성 후 당도를 생성 | 설의 숙성 후 당도($_1^2Y_2$): = $_1^2Y_1 + {_1\bar {D}}$ + (NORMINV(RAND(), 0, 0.1)) | 아키의 숙성 후 당도($_2^2Y_2$): = $_2^2Y_1 + {_2\bar {D}}$ + (NORMINV(RAND(), 0, 0.1)) |
| 당도 $(^1y)$ | 생성 모델에 따라 성숙일에 기울기를 곱하고 오차를 추가하여 당도를 생성 | 설의 당도($_1^2Y$): = $0.3\times {_1^2X}$ + (NORMINV(RAND(), 0, 0.25)) | 아키의 당도($_2^2Y$): = $0.25\times {_2^2X}$ + (NORMINV(RAND(), 0, 0.5)) |
| 과중 $(^2y)$ | 생성 모델에 따라 성숙일에 기울기를 곱하고 오차를 추가하여 과중을 생성 | 설의 과중($_1^1Y$): = $0.6\times {_1^2X}$ + (NORMINV(RAND(), 0, 0.25)) | 아키의 과중($_2^1Y$): = $0.5\times {_2^2X}$ + (NORMINV(RAND(), 0, 0.25)) |
Table 5에서 합성데이터를 생성한 모델의 매개변수와 생성된 데이터의 통계량을 비교하였다. 당도와 과중의 평균과 표준편차에 있어서 매개변수와 생성된 데이터의 통계량 사이의 차이는 각각 0.01 Brix, 0.01 g 이하이다.
Table 5. Comparison of parameters used for synthetic data generation and statistics of the generated data
| Cultivar | Comparison | Sweetness (Brix) | Weight (g) | Sweetness after cold aging (Brix) |
|---|---|---|---|---|
| Seol | Parameter | 10.80 ± 0.65 | 21.60 ± 1.24 | 11.00 ± 0.66 |
| Statistic | 10.80 ± 0.66 | 21.59 ± 1.24 | 11.00 ± 0.66 | |
| Aki | Parameter | 9.00 ± 0.71 | 18.00 ± 1.04 | 9.10 ± 0.72 |
| Statistic | 9.00 ± 0.71 | 17.99 ± 1.03 | 9.10 ± 0.72 |
Mean ± standard deviation.
The mean has been rounded to the second decimal place and the standard deviation has been rounded to the second decimal place.
Figure 1에서는 생성모델에서 정한 확률분포와 실제 생성된 데이터의 히스토그램을 함께 표시하여, 설과 아키의 당도, 과중, 저온숙성 후 당도의 분포를 비교할 수 있도록 하였다.
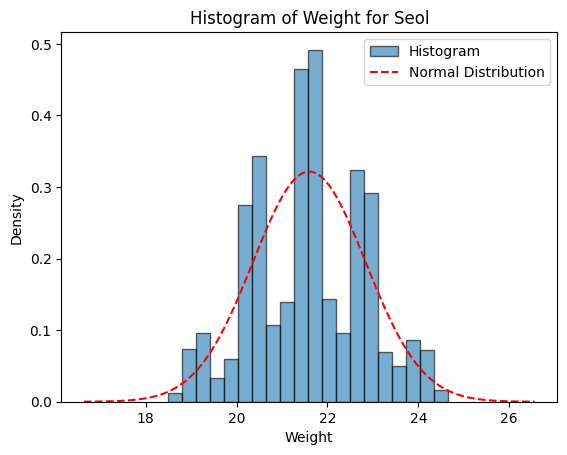
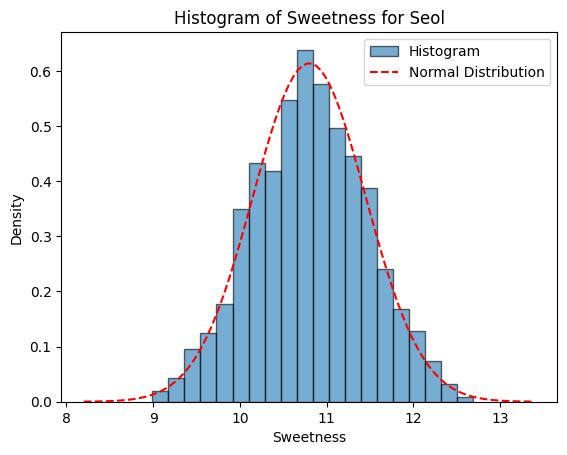
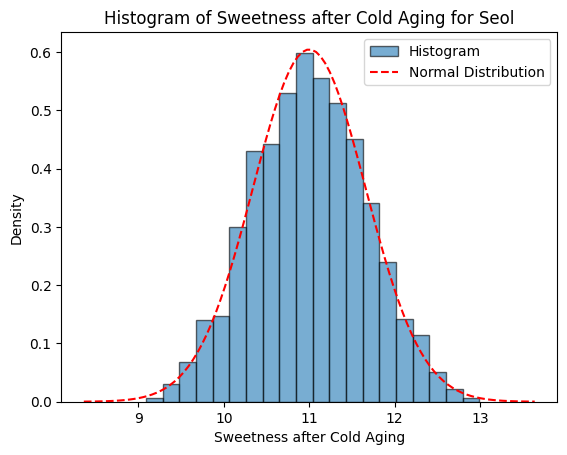
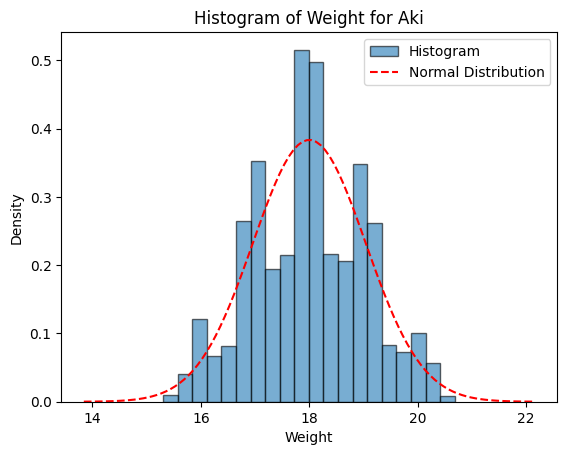
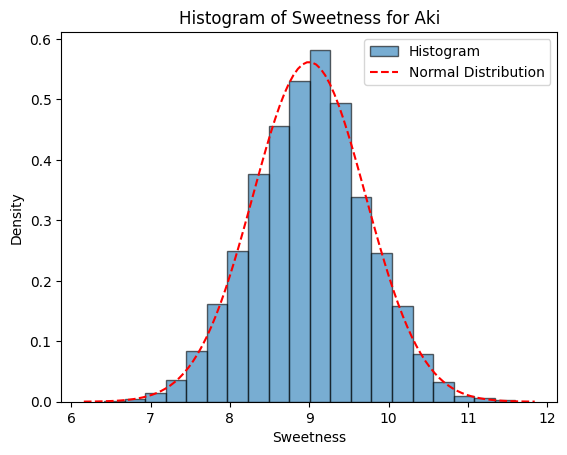
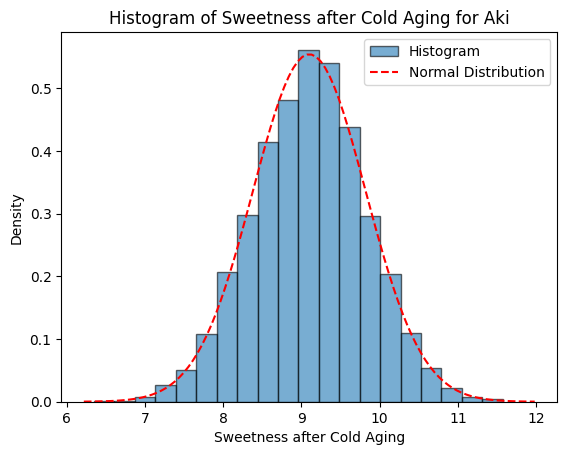
Figure 1. Normal distribution of the generative model and histograms of the generated data. A, Seols’ weiight (g); B, Seols’ sweetness (Brix); C, Seols’ sweetness after cold aging (Brix); D, Akis’ weiight (g); E, Akis’ sweetness (Brix); F, Akis’ sweetness after cold aging (Brix).
생성모델에 따른 합성 데이터 생성에는 구글시트를 사용하였으며, 생성된 데이터와 생성모델의 정규분포 모델의 시각적 비교는 구글코랩을 사용하였다. 각각의 코드는 아래의 URL에서 접근할 수 있다.
구글시트: https://docs.google.com/spreadsheets/d/1965P4ni1xCcmDz7KU7s97kanlYdAp3qn7OQHCyB1nZc/
구글코랩: https://colab.research.google.com/drive/1t_9pgyzkljh4tcjnyFSJH7pkCzNBUy8x
데이터는 아래의 URL에서 접근할 수 있다.
구글시트: https://docs.google.com/spreadsheets/d/1965P4ni1xCcmDz7KU7s97kanlYdAp3qn7OQHCyB1nZc/
이 연구를 위해 지원을 해 주신 관련 기관 및 개인들께도 도움 덕분에 본 연구는 성공적으로 완료될 수 있었다. 다시 한번 감사의 인사를 드린다.
Geun Cheol Park: 주요 모델 설계, 데이터 생성과 논문 초안 작성.
Yun-Won Yang: 모델 설계 리뷰, 논문 초안 작성과 최종 검토.
1. Park GC, Yang YW. 2024. The product value of strawberry. DataLink Forum 2024:p1. https://doi.org/10.12972/DataLink.2024.p1
2. Liu F, Panagiotakos D. 2022. Real-world data: a brief review of the methods, applications, challenges and opportunities. BMC Medical Research Methodology 22:287. https://doi.org/10.1186/s12874-022-01768-6
3. Anagnostopoulos C, Devereson A, El Turabi A, et al. 2023. Real-world data quality: What are the opportunities and challenges? Accessed in https://www.mckinsey.com/industries/life-sciences/our-insights/real-world-data-quality-what-are-the-opportunities-and-challenges on 6 July 2024.
4. Anderson C. 2016. Real-world data collection: Prioritizing and evaluating data sources for ROI. Accessed in https://www.oreilly.com/content/real-world-data-collection/ on 6 July 2024.
5. Timonera K. 2024. 11 Top Data Collection Trends Emerging In 2024. Accessed in https://www.datamation.com/big-data/data-collection-trends/ on 6 July 2024.
6. Ramalho Marques JM, Torres AP, Behe BK, et al. 2021. Exploring Consumers’ Preferred Purchase Location for Fresh Fruits. HortTechnology 31(5):595-606. https://doi.org/10.21273/HORTTECH04865-21
7. Burrill G, Pfannkuch M. 2024. Emerging trends in statistics education. ZDM Mathematics Education 56:19–29. https://doi.org/10.1007/s11858-023-01501-7
8. Schreiter S, Friedrich A, Fuhr H, et al. 2024. Teaching for statistical and data literacy in K-12 STEM education: a systematic review on teacher variables, teacher education, and impacts on classroom practice. ZDM Mathematics Education 56:31–45. https://doi.org/10.1007/s11858-023-01531-1
9. Jo JS, Kim DS, Jo WJ, ey al. 2022. Prediction of strawberry fruit yield based on cultivar-specific growth models in the tunnel-type greenhouse. Horticulture, Environment, and Biotechnology 63:467–476. https://doi.org/10.1007/s13580-021-00416-0
10. Middle Class. 2024. 10 Korean Strawberry Varieties: Seolhyang, King’s Berry, Sancheong & More. Accessed in https://middleclass.sg/treats/korean-strawberry-varieties/ on 9 October 2024.
11. Jubilee. 2023. Exploring Delights of the World: Sweet Indulgence of Korean Strawberries. Accessed in https://www.jubileemarketplace.com/news-item/exploring-delights-of-the-world-sweet-indulgence-of-korean-strawberries/ on 9 October 2024.
본인의 Google 계정으로 구글시트를 복사
본인의 Google 계정으로 구글코랩을 복사