COURSE : 초등학생의 수학적 창의력

ROUTINE 가설검정 논문작성 PROGRAMMING PROJECT 대응표본 t검정 독립표본 t검정 일원분산분석 F검정 상관분석 t검정 단순선형회귀분석 F검정 교차분석 카이제곱검정 초등학생의 수학적 창의력 논문작성 DATA SET 프로젝트 데이터셋 P3-project-data 구글시트 모집단 데이터셋 표본 추출 표본 데이터셋 P3-1-data 구글시트 ARTICLE [ PROJECT ] 딸기의 상품가치 Project DocuHut Full Text [ DATA ] 데이터사이언스 학습을 위해 생성한 가상 딸기 데이터셋 […]

모든 집단의 평균이 같을 때, 모집단내 “집단간분산”과 “집단내분산”이 같은 이유는?

[ QA ] CONTENTS “집단내변동”만으로 두 분산이 정해지기 때문입니다. 모든 집단의 평균이 같다면 “집단간변동”은 없습니다. 분산분석(ANOVA)의 기본 개념 총변동($SS_T$)은 전체 데이터의 변동성을 나타내며, 집단간변동($SS_B$)과 집단내변동($SS_W$)의 합으로 표현됩니다. $$SS_T=SS_B+SS_W$$ $MS_B$은 집단간분산이며 집단평균의 변동입니다. 집단간변동과의 관계는 다음식으로 표현됩니다 $$MS_B = dfrac{SS_B}{text{집단간 자유도}}$$ $MS_W$은 집단내분산이며 각 집단내에서 데이터의 변동입니다. 집단내변동과의 관계는 다음식으로 표현됩니다. $$MS_W = dfrac{SS_W}{text{집단내 자유도}}$$​ 등분산 […]

모집단에서 집단간분산과 집단내분산이 동일해지는 경우는?

CONTENTS 모집단내 각 집단의 모평균이 같을 때 입니다. 이 경우, 집단간분산과 집단내분산은 모집단의 분산을 추정합니다. 무한 모집단(population) 내 각 집단(group)의 크기도 무한대입니다. 모집단내 집단의 변동 모집단에서 무작위로 표본을 추출할 때, 그 표본이 충분히 크면, 즉, 표본의 크기가 무한대에 가까워지면, 그 표본은 모집단의 특성을 정확하게 반영합니다. 아찬가지로 모집단내 집단 간의 평균이 같을 때 집단간 변동의 차이는 […]

일원분산분석에서 F통계량, F검정통계량, F검정통계값의 관계는?

CONTENTS 귀무가설을 통해 , F통계량의 변수의 수를 줄여 F검정통계량을 구합니다. 여기서, 귀무가설은 알 지 못하는 모수에 대한 가설입니다. F검정통계량은 확률변수이며 정의된 확률분포함수로 표현합니다. 표본데이터를 통해, F검정통계량의 함수값인 F검정통계값을 구합니다. 일원분산분석에서 F통계량 일원분산분석에서의 F통계량을 함수로 보면 다음과 같이 표현할 수 있습니다. $$F(chi^2_B, df_B, chi^2_W, df_W) = dfrac{dfrac{chi^2_B}{df_B}}{dfrac{chi^2_W}{df_W}}= dfrac{dfrac{S_{B}^2}{sigma_{B}^2}}{dfrac{S_{W}^2}{sigma_{W}^2}}$$ 여기서, $chi^2_B$는 표본내 집단의 카이제곱: $chi^2_B=df_Bdfrac{S_B^2}{sigma_B^2}$ $chi^2_W$는 표본내 […]

용어 – Wikipedia

TERMS 데이터 데이터는 질적 또는 양적 변수값의 집합입니다. 데이터와 정보 또는 지식은 종종 같은 의미로 사용하지만 데이터를 분석하면 정보가 된다고 볼 수 있습니다. 데이터는 일반적으로 연구의 결과물로 얻어집니다. 한편, 데이터는 경제(매출, 수익, 주가 등), 정부(예 : 범죄율, 실업률, 문맹율)와  비정부기구(예 : 노숙자 인구 조사)등 다양한 분야에서도 나타납니다. 그리고 데이터를 수집 및 분석하고 시각화할 수 있습니다. 일반적인 […]

한우의 품질

CONTENTS Author Detail Publication Histroy DOI Citation Download Print 구글문서 MS워드 Print 구글문서 MS워드 요약 이번 프로젝트의 목적은 한우 품질 평가를 위해 확률 모델을 사용하여 데이터셋을 생성하고, p-값을 기반으로 가설을 검정하는 과정을 개발하는 것입니다. 국내 한우 품종을 대상으로 근육내 지방 함량(근내 지방도), 도체 중량, 및 등심 단면적을 결과변수로 설정하고, 근육 부위(등심, 설도), 지역별 도체 중량, […]

t통계량, t검정통계량, t검정통계값의 관계는?

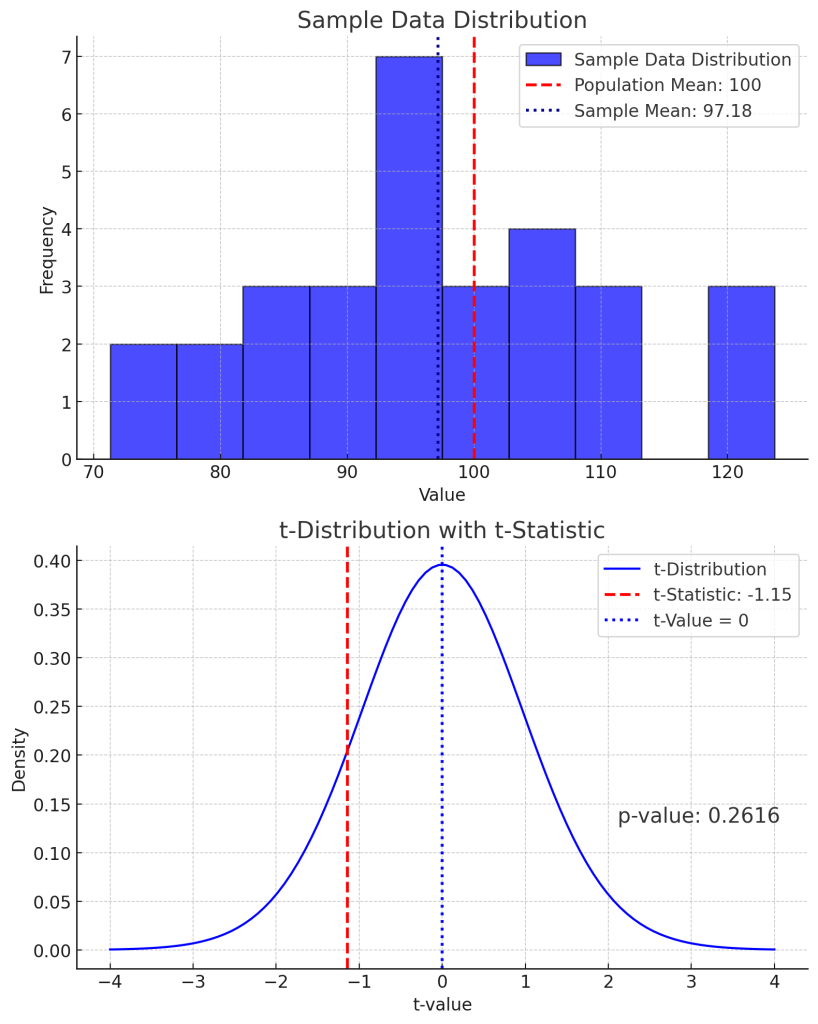
CONTENTS 귀무가설을 통해 , t통계량의 변수의 수를 줄여 t검정통계량을 구합니다. 여기서, 귀무가설은 알 지 못하는 모수에 대한 가설입니다. t검정통계량은 확률변수이며 정의된 확률분포함수로 표현합니다. 표본데이터를 통해, t검정통계량의 함수값인 t검정통계값을 구합니다. t통계량, t검정통계량, t검정통계값의 관계 t통계량을 함수로 보면 다음과 같습니다. $$t(bar{X}, mu, s, n) = dfrac{bar{X} – mu}{dfrac{s}{sqrt{n}}}$$ 여기서, $t$는 t통계량 $nu$는 자유도: $nu=n-1$ $n$은 표본크기 $Gamma(,,,)$는 […]

표본통계량의 표집분포

Animation Figure 데이터종류 데이터 수집 데이터 종류 데이터종류 데이터 수집 데이터 종류 [Q&A] 스프레드시트에서 정리한 정형데이터에서 데이터를 속성에 따라 분류하면 범주형데이터, 순서있는 범주형데이터, 이산형데이터, 연속형데이터 이 중에서 이산형데이터와 연속형데이터는 수치로 나타나는 양적데이터입니다.  범주형데이터, 순서있는 범주형데이터, 이산형데이터, 연속형데이터 이 중에서 이산형데이터와 연속형데이터는 수치로 나타나는 양적데이터입니다.  데이터 프레임 데이터 프레임은 열과 행으로 구성된 테이블 형태의 데이터 구조로, […]

비모수 가설검정

TABLES 중앙값의 부호 검정 – 표본크기가 큰 경우 : 검정통계량이 Z.분포를 따름 귀무가설($H_0$) 검정통계량 대립가설($H_1$) 귀무가설 기각역 $M=M_0$ $n_{+}=’+{rm 부호의} {rm 갯수}’$ $M> M_0$ $dfrac{n_{+}-0.5n}{sqrt{0.25n}}> z_{alpha}$ $M< M_0$ $dfrac{n_{+}-0.5n}{sqrt{0.25n}}<-z_{alpha}$ $Mne M_0$ $left|dfrac{n_{+}-0.5n}{sqrt{0.25n}}right|> z_{frac{alpha}{2}}$ 중앙값의 부호 검정 – 표본크기가 작은 경우 : 귀무가설$(H_0)$ 검정통계량 대립가설$(H_1)$ 귀무가설 기각역 $$M=M_0$$ $$n_{+}=’+{rm 부호의} {rm 갯수}’$$ $$M> M_0$$ $$n_{+}> B{left({n,0.5}right)}_{alpha}$$ $$M< […]

표본분산의 표집분포

Animation Figure CONTENTS Author Detail Publication Histroy DOI Citation Download Print 구글문서 Print 구글문서 Abstract 표본분산의 표집분포는 모집단에서 여러 번 표본을 추출해 각각의 표본분산을 계산한 결과로 이루어진 분포입니다. 확률변수가 정규분포를 따를 때, 표본분산에 자유도를 곱하고 모분산으로 나눈 새로운 확률변수는 카이제곱 분포를 따르며, 이는 모집단의 분산을 추정하는 데 활용됩니다. 표본분산을 계산할 때, 자유도를 고려해 표본 크기에서 […]