연속형 확률변수가 유리수로 실현될 확률은?
CONTENTS 연속형 확률변수가 유리수로 실현될 확률은 0입니다. 연속형 확률변수가 무리수로 실현될 확률은 1입니다. 실수의 확률공간 실수는 유리수와 무리수로 구성됩니다. $$mathbb{R} = mathbb{Q} cup (mathbb{R} setminus mathbb{Q})$$ 여기서, $mathbb{R}$은 실수 $mathbb{Q}$는 유리수 $(mathbb{R} setminus mathbb{Q})$은 무리수: $mathbb{R}$집합에서 $ mathbb{Q}$집합을 뺀 집합 유리수와 무리수는 서로소(disjoint) 관계인 배타적인 집합입니다. $$mathbb{Q} cap (mathbb{R} setminus mathbb{Q}) = emptyset$$ 여기서, $emptyset$은 […]
확률이론에서 표본공간과 벡터공간을 연결하는 함수는?
CONTENTS 양적 확률변수(quantitative random variable) 또는 양적 확률벡터(quantitative random vector)입니다. 확률변수 또는 확률벡터를 함수라고 하는 이유는 표본공간의 원소를 벡터공간의 점 또는 점의 집합으로 변환하는 기능을 하기 때문입니다. 확률변수를 기호로 표현하면 다음과 같습니다. $$X : Omega to mathbb{R}$$ 여기서, $X$는 양적(수치형) 확률변수 $Omega$는 표본공간 $mathbb{R}$는 $1$차원 벡터공간 확률벡터를 기호로 표현하면 다음과 같습니다. $$X : Omega to […]
확률이론에서의 표본과 통계학에서의 표본은 의미가 같은가?
CONTENTS 아니오, 용어는 같지만 의미는 다릅니다. 확률이론에서의 표본은 표본공간의 원소로서 더 이상 나눌 수 없는 사건의 결과입니다. 통계학에서의 표본은 모집단의 부분집합으로서 모집단의 특성을 추정합니다. 확률이론에서의 표본 확률이론(probability theory)에서는 확률공간(probability space)으로 확률(probability)을 설명합니다. 확률공간의 3요소는 표본공간(sample space), 시그마대수($sigma$-algebra), 확률측도(probility measure) 입니다. 표본공간에서 나올 수 있는 단일 결과를 표본(sample)이라고 합니다. 이는 더 이상 나눌 수 없는 개별적인 […]
모든 집단의 평균이 같을 때, 모집단내 “집단간분산”과 “집단내분산”이 같은 이유는?
[ QA ] CONTENTS “집단내변동”만으로 두 분산이 정해지기 때문입니다. 모든 집단의 평균이 같다면 “집단간변동”은 없습니다. 분산분석(ANOVA)의 기본 개념 총변동($SS_T$)은 전체 데이터의 변동성을 나타내며, 집단간변동($SS_B$)과 집단내변동($SS_W$)의 합으로 표현됩니다. $$SS_T=SS_B+SS_W$$ $MS_B$은 집단간분산이며 집단평균의 변동입니다. 집단간변동과의 관계는 다음식으로 표현됩니다 $$MS_B = dfrac{SS_B}{text{집단간 자유도}}$$ $MS_W$은 집단내분산이며 각 집단내에서 데이터의 변동입니다. 집단내변동과의 관계는 다음식으로 표현됩니다. $$MS_W = dfrac{SS_W}{text{집단내 자유도}}$$ 등분산 […]
모집단에서 집단간분산과 집단내분산이 동일해지는 경우는?
CONTENTS 모집단내 각 집단의 모평균이 같을 때 입니다. 이 경우, 집단간분산과 집단내분산은 모집단의 분산을 추정합니다. 무한 모집단(population) 내 각 집단(group)의 크기도 무한대입니다. 모집단내 집단의 변동 모집단에서 무작위로 표본을 추출할 때, 그 표본이 충분히 크면, 즉, 표본의 크기가 무한대에 가까워지면, 그 표본은 모집단의 특성을 정확하게 반영합니다. 아찬가지로 모집단내 집단 간의 평균이 같을 때 집단간 변동의 차이는 […]
표본통계량의 표집분포
Animation Figure 데이터종류 데이터 수집 데이터 종류 데이터종류 데이터 수집 데이터 종류 [Q&A] 스프레드시트에서 정리한 정형데이터에서 데이터를 속성에 따라 분류하면 범주형데이터, 순서있는 범주형데이터, 이산형데이터, 연속형데이터 이 중에서 이산형데이터와 연속형데이터는 수치로 나타나는 양적데이터입니다. 범주형데이터, 순서있는 범주형데이터, 이산형데이터, 연속형데이터 이 중에서 이산형데이터와 연속형데이터는 수치로 나타나는 양적데이터입니다. 데이터 프레임 데이터 프레임은 열과 행으로 구성된 테이블 형태의 데이터 구조로, […]
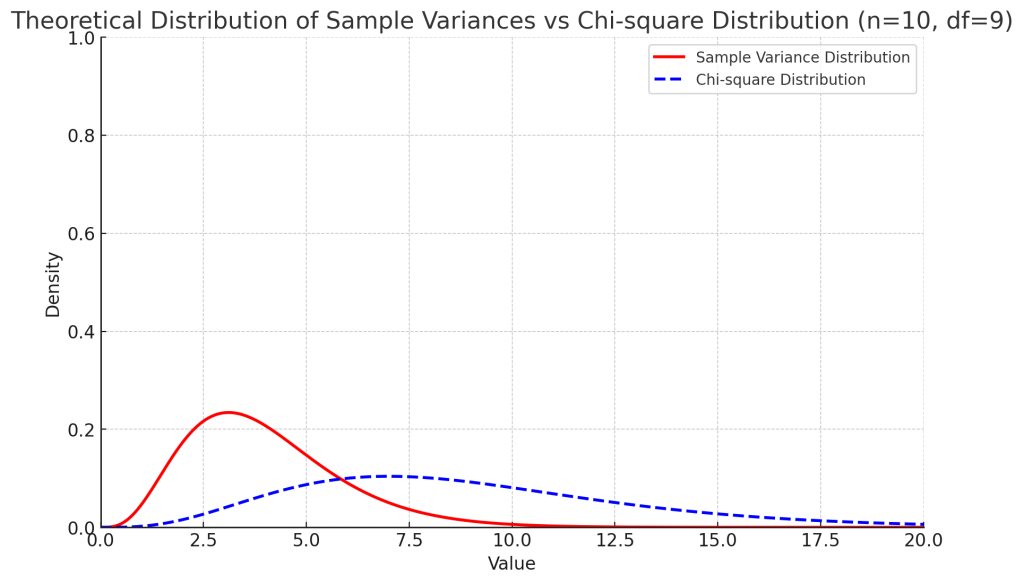
표본분산의 표집분포
Animation Figure CONTENTS Author Detail Publication Histroy DOI Citation Download Print 구글문서 Print 구글문서 Abstract 표본분산의 표집분포는 모집단에서 여러 번 표본을 추출해 각각의 표본분산을 계산한 결과로 이루어진 분포입니다. 확률변수가 정규분포를 따를 때, 표본분산에 자유도를 곱하고 모분산으로 나눈 새로운 확률변수는 카이제곱 분포를 따르며, 이는 모집단의 분산을 추정하는 데 활용됩니다. 표본분산을 계산할 때, 자유도를 고려해 표본 크기에서 […]
집단간분산과 집단내분산이 같다는 것은?

[ QA ] CONTENTS 범주형 원인변수에 의한 분산과 내재된 분산이 같다는 의미입니다. 신호와 노이즈의 양이 같다는 의미입니다. 집단간분산이 집단내분산보다 작은 구역은 중첩되어 있는 영역입니다. 큰 영역은 확실히 범주형 원인변수가 작동하는 영역입니다. 집단간분산과 집단내분산은 무엇? 집단간분산(Between-Group Variance)은 서로 다른 집단의 평균값 차이를 설명합니다. 즉, 각 집단의 평균이 전체 평균(또는 다른 집단의 평균)과 얼마나 차이가 나는지를 나타냅니다. […]
표본분산을 카이제곱으로 변환하는 이유는?
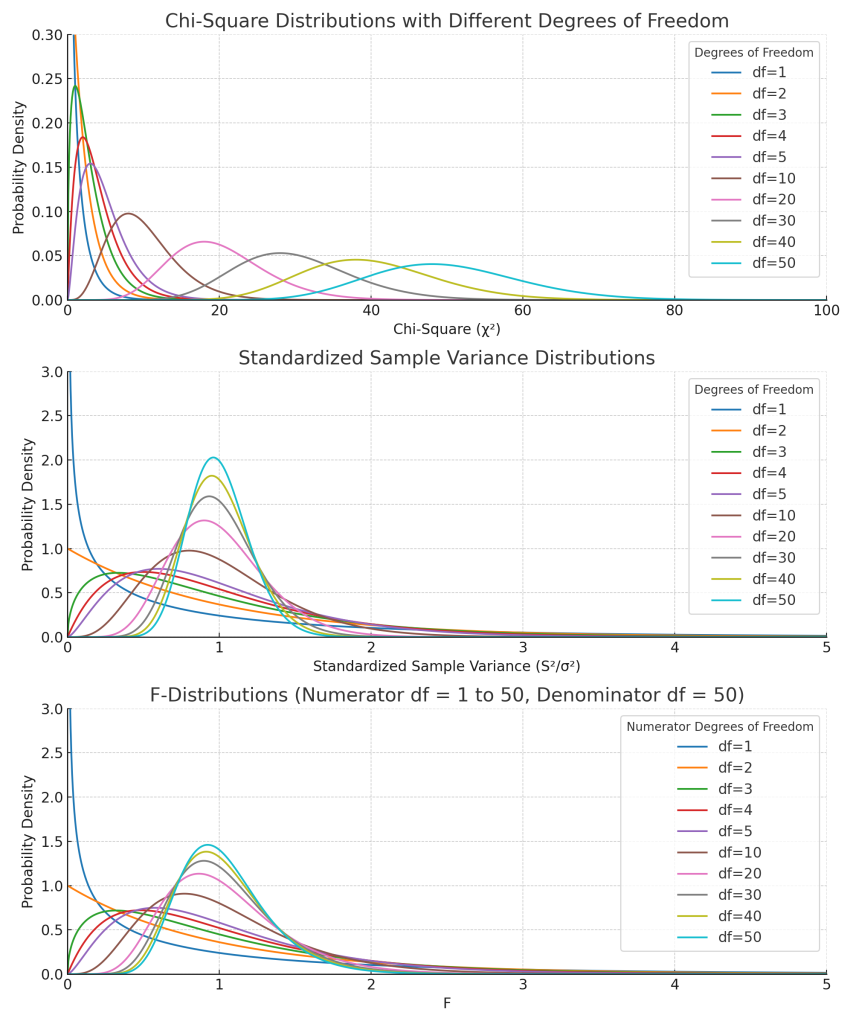
[ QA ] CONTENTS 카이제곱은 표준정규분포에서 유도된 확률분포를 가지기 때문입니다. 표본분산을 카이제곱변환하는 과정에서 자유도의 정보가 포함됩니다. 유사하게, 표본평균을 Z변환하는 과정에서 표본크기의 정보가 포함됩니다. 확률변수의 확률분포: 정규분포로 모델링 확률변수의 확률분포: 정규분포로 모델링 $$Y sim N(mu_Y, sigma^2_Y)$$ 여기서, $Y$는 확률변수 $N(mu_Y, sigma^2_Y)$는 $mu_Y$와 $sigma^2_Y$를 매개변수로 하는 정규분포 $mu_Y$는 확률변수 $Y$의 모평균 $sigma^2_Y$는 확률변수 $Y$의 모분산 확률변수의 확률밀도함수 […]
표준오차를 꼭 필요로 하는 표본통계량 순서는?
[ QA ] CONTENTS 표본평균, 표본비율, 표본분산의 순입니다. 표준오차는 무엇? 표준오차(Standard Error, SE)는 통계에서 표본평균, 표본분산, 표본비율 등의 표본 통계량이 반복적인 표본추출에서 모평균, 모분산, 모비율가 얼마나 차이가 나는 지를 나타냅니다. 즉, 표본 통계량의 모수에 대한 변동성을 나타내는 척도입니다. 표준오차는 왜 생기나? 표준오차는 표본추출 과정에서 발생하는 변동성으로 설명됩니다. 표본추출이 무작위적이므로, 각 표본에서 계산된 통계량이 다를 수밖에 없으며, […]

