Menu
Menu
ROUTINE : 12
PROJECT : 2
PROGRAMMING : 6
eISBN
eISSN
Menu
대응된 집단 2개
변동: 모수병진이동$(d_0)$ + 모수회전
$\bar D$
여기서, $\bar D$는 대응된 원소의 차이평균:
$\bar{d}=\bar{y}_{1\cdot }-\bar {y}_{2\cdot }$
$d_i=y_{1i} – y_{2i}$
$d_i$는 집단1과 집단2의 $i$번째 대응된 원소의 차이
$\bar d=\dfrac{\sum\limits_{i=1}^n di}{n}$
$$\text{SE}(\bar D)=\sqrt{\dfrac{\sum\limits_{i=1}^{n}(\bar d_{1i} – \bar d_{2i})^2}{n}}=\dfrac{s_D}{\sqrt{n}}$$
여기서, $n$은 대응된 쌍의 수
대응된 두 집단의 모평균의 차이는 $d_0$이다.
$$\mu_{Y_1}-\mu_{Y_2}=d_0$$
$$t = \dfrac{\bar d-d_0}{\dfrac{s_D}{\sqrt{n}}}$$
여기서, $\bar d$는 차이평균의 관측값:
$\bar{d}=\bar{y}_{1\cdot }-\bar {y}_{2\cdot }$
$\bar{y}_{1 \cdot}$, $\bar{y}_{2 \cdot}$는 대응된 두 집단 표본평균의 관측값
$d_0$는 귀무가설로 주어지는 모평균차이: $\mu_{Y_1}-\mu_{Y_2}=d_0$
$s_D$는 확률변수 $D$의 표본표준편차
$n$은 대응표본크기(대응쌍의 수)
$t_{n}$
여기서, $n$은 대응된 쌍의 수
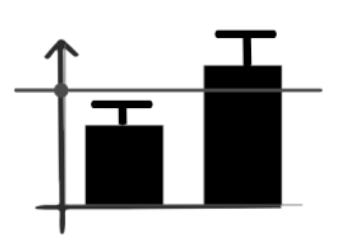
독립된 집단 2개
변동: 모수병진이동(bias=$d_0$)+모수회전(독립, 등분산가정 $\therefore$ 기울기=0)
등분산아닌 경우: 웰치t검정
$$\bar{D}$$
여기서, $\bar{D}$는 평균차이:
$\bar{d}=\bar{y}_{1}-\bar{y}_{2}$
$$\text{SE}(\bar D)=s_p \sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}}$$
여기서, $s_p$는 통합표준편차:
$s_p=\sqrt{\dfrac{(n_1-1)s_1^2+(n_2-1)s_2^2}{n_1+n_2-2}}$
독립된 두 집단의 모평균의 차이는 $d_0$이다.
$\mu_{Y_1} – \mu_{Y_2}=d_0$
독립된 두 집단의 모평균이 같다.
$\mu_{1}=\mu_{2}=\mu_0$
$\beta_{0,1}=\beta_{0,2}=\beta_0$
$$\therefore \sigma_B^2=0$$
$$t =\dfrac{\bar d-d_0}{s_p \sqrt{\dfrac{1}{n_1} + \dfrac{1}{n_2}}}$$
여기서, $\bar d$는 평균차이의 관측값:
$\bar{d}=\bar{y}_{1}-\bar{y}_{2}$
$\bar{y}_{1}$, $\bar{y}_{2}$는 독립된 두 집단의 표본평균의 관측값
$d_0$는 귀무가설로 주어지는 모평균차이: $d_0=\mu_{Y_2}-\mu_{Y_1}$
$n_1$, $n_2$는 독립된 두 집단의 표본크기: $n_1+n_2=n$
$n$은 전체표본크기: $n=n_1+n_2$
$t=\sqrt{F}=\sqrt{\dfrac{s_{B}^2}{s_{W}^2}}=\sqrt{\dfrac{MS_{B}}{MS_{W}}}$
$\sigma_B^2 \neq 0$인 경우 $\sigma_B^2 $과 $\sigma_W^2$의 크기 비교
$t_{n_1+n_2-2}$
여기서, $n_1$, $n_2$는 각각 표본내 집단1과 집단2의 크기
$n=n_1+n_2$
표본크기$(n)$은 표본크기
$t_{n-k}$
여기서, $n$은 표본크기
$n=n_1+n_2$
$n_1$, $n_2$는 각각 표본내 집단1과 집단2의 크기
$k$는 표본내 집단의 수: k=2
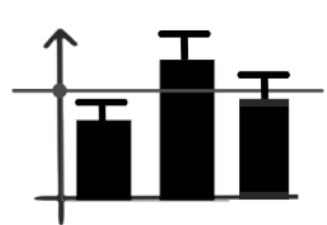
독립된 집단 2개이상
변동: 모수병진이동(bias=$d_0$)+모수회전(독립, 등분산가정 $\therefore$ 기울기=0)
$MS_{reg}$
$MS_{res}$
독립된 여러 집단의 모평균($\mu_i$)이 같다.
$\mu_{1}=\mu_{2}=\cdots=\mu_{k}=\mu_0$
$\beta_{0,1}=\beta_{0,2}=\cdots=\beta_{0,k}=\beta_0$
여기서, $\mu_i$는 $i$번째 집단의 모평균
$\beta_{0,i}$는 $i$번째 집단의 모평균
$k$는 표본내 집단의 수
$F=\dfrac{s_{B}^2}{s_{W}^2}=\dfrac{MS_{B}}{MS_{W}}$
$\sigma_B^2 \neq 0$인 경우 $\sigma_B^2 $과 $\sigma_W^2$의 크기 비교
$F_{k-1, n-k}$
여기서, $n$은 표본크기
$k$는 표본내 집단의 수
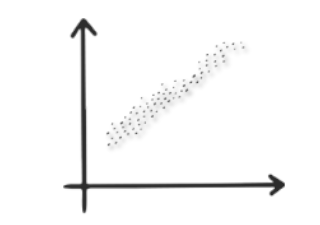
집단 2개: 회귀와 잔차
변동: 모수회전
$r$
여기서, $r$은 표본상관계수:
두 변수인 경우 $r^2=R^2$
$R^2$은 표본결정계수
$$\text{SE}(r)=\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}$$
$\rho=\rho_0$
$$t=\dfrac{r-\rho_0}{\dfrac{\sqrt{1-r^2}}{\sqrt{n-2}}}$$
여기서, $\rho_0$는 모상관계수
표본의 두 집단의 상관관계가 없으면 $\rho_0=0$
$r$은 표본상관계수: $r=\dfrac{s_{XY}}{s_{X}s_{Y}}$
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{R^2}{2-1}}{\dfrac{1-R^2}{n-2}}∼F_{1,n-2}$$
여기서, $R^2=\dfrac{s^2_{XY}}{s^2_{X}s^2_{Y}}$
$t_{n-2}$
여기서, $n$은 표본크기: 대응된 쌍의 수
$F_{1, n-2}$
여기서, $n$은 표본크기: 대응된 쌍의 수
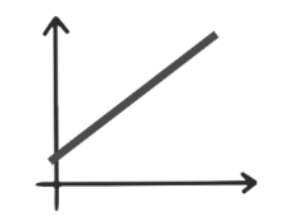
집단 2개: 회귀와 잔차
변동: 모수회전
$R^2$
여기서, $R^2$은 표본결정계수:
두 변수인 경우 $R^2=r^2$
$r$은 표본상관계수
$$\text{SE}(R^2)=\dfrac{1-R^2}{n-2}$$
$$ \beta_1=\beta_{1,0}$$
$$F=\dfrac{MS_{Reg}}{MS_{Res}}=\dfrac{\dfrac{R^2}{2-1}}{\dfrac{1-R^2}{n-2}}∼F_{1,n-2}$$
여기서, $R^2=\dfrac{s^2_{XY}}{s^2_{X}s^2_{Y}}$
$F_{1, n-2}$
여기서, $n$은 표본크기: 대응된 쌍의 수
집단 $r\times c$개: 교차점수
변동: 분포
$$\sum\limits_{\text{교차점}}(\text{결합확률}-\text{주변확률}_1 \times \text{주변확률}_2)^2$$
$$\sum\limits_{\text{교차점}}(\text{주변확률}_1 \times \text{주변확률}_2)^2$$
$\chi_{obs}^2=0$
$\chi_{obs}^2=\sum\limits_{i=1}^{r}\sum\limits_{j=1}^{c}\dfrac{(O_{ij}-E_{ij})^2}{E_{ij}}$
$\chi^2_{(r-1)(c -1)}$
여기서, $r$은 한 범주형 변수의 변수값의 수
$c$은 다른 범주형 변수의 변수값의 수
$(r-1)(c-1)$은 자유도