[ Q&A ]

확률이론에서의 표본과 통계학에서의 표본은 의미가 같은가?

아니오, 용어는 같지만 의미는 다릅니다.

확률이론에서의 표본은 표본공간의 원소로서 더 이상 나눌 수 없는 사건의 결과입니다.

통계학에서의 표본은 모집단의 부분집합으로서 모집단의 특성을 추정합니다.

확률이론에서의 표본

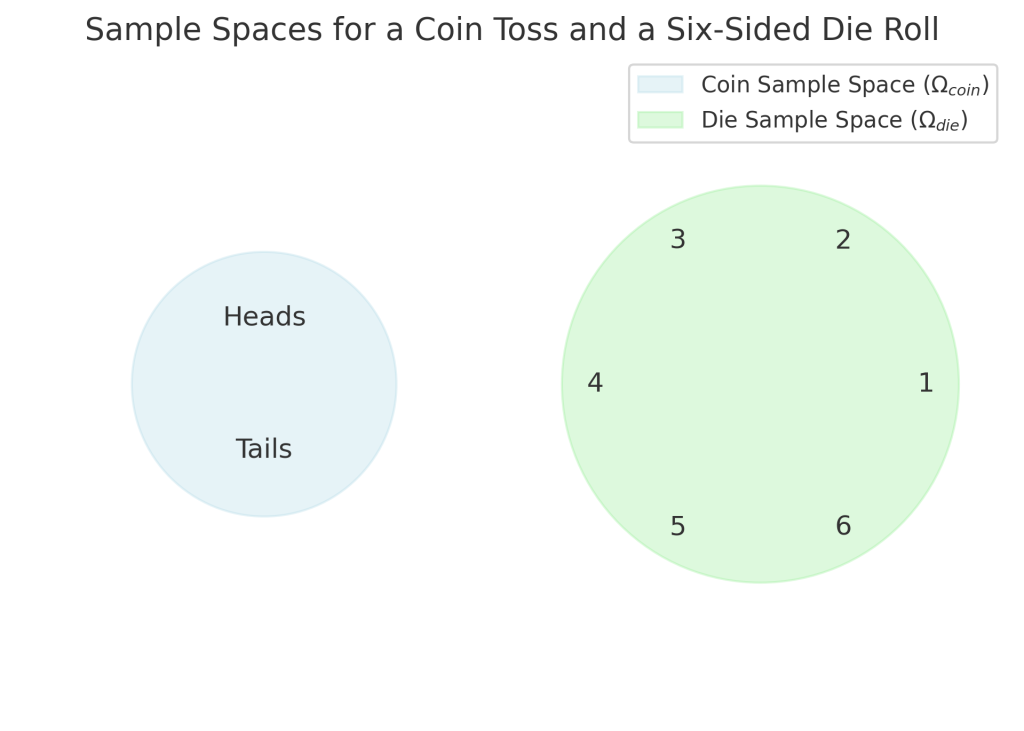
확률이론(probability theory)에서는 확률공간(probability space)으로 확률(probability)을 설명합니다. 확률공간의 3요소는 표본공간(sample space), 시그마대수($\sigma$-algebra), 확률측도(probility measure) 입니다. 표본공간에서 나올 수 있는 단일 결과를 표본(sample)이라고 합니다. 이는 더 이상 나눌 수 없는 개별적인 사건의 결과입니다. 예를 들어, 동전을 한 번 던졌을 때 나오는 “앞”이나 “뒤”, 주사위를 한 번 던졌을 때 나오는 특정 숫자(예: 3)가 표본입니다. 표본공간의 표본은 각각 고유한 결과를 나타내며, 확률적 사건을 정의하는 기본 단위입니다. 표본공간에서의 표본을 표본점(sample point)이라고 부르기도 합니다.

확률공간의 세가지 요소

확률공간(probability space)은 표본공간(sample space, $\Omega$), 시그마대수($\sigma$-algebra), 확률측도(probability measure, $P$)로 구성됩니다.

표본공간은 가능한 모든 단일 결과인 표본들의 집합입니다.
시그마대수는 표본공간($\Omega$)의 부분집합들을 원소로 하는 집합으로, 이 부분집합을 사건(event)이라고 부릅니다. 따라서 시그마대수를 사건을 원소로 하는 집합이라고 할 수 있습니다. 시그마대수는 표본공간 위에서 정의할 수 있는 여러 가지 선택 가능한 집합의 모임으로, 목적에 따라 사건을 선택하여 구성할 수 있습니다. 시그마대수는 확률을 정의할 수 있는 사건의 범위를 설정하는 도구라고 할 수 있습니다. 가장 큰 시그마대수에는 표본공간의 모든 부분집합을 포함하는 멱집합이 있습니다. 그리고 특정한 사건들에 대한 정보만 필요할 경우, 더 작은 시그마대수를 구성할 수 있습니다. 예를 들어, 주사위를 던질 때 짝수와 홀수만을 고려한 시그마대수를 만들 수 있습니다. 시그마대수는 여집합, 가산 합집합, 그리고 결과적으로 가산 교집합에 대해 닫혀 있어야 합니다. 시그마대수는 사건공간(a space of events, $\mathcal{F}$)이라고 부르기도 합니다.
확률측도는 사건에 확률을 할당하는 함수입니다.

통계학에서의 표본

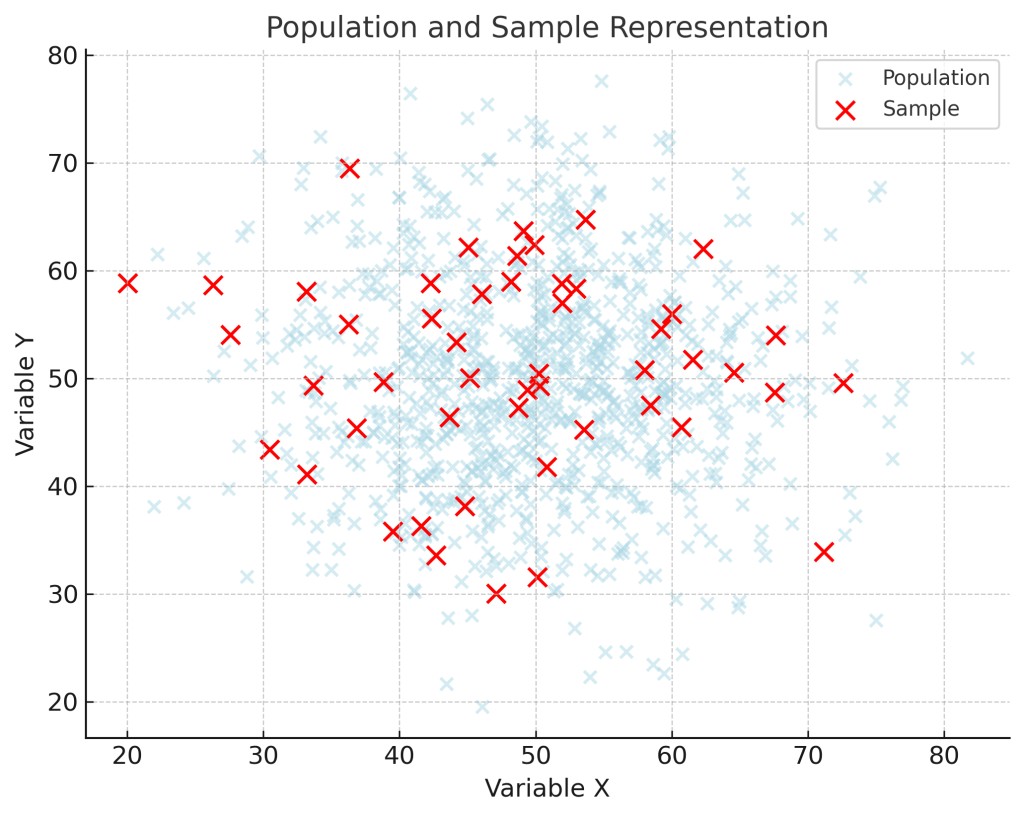
통계학(statistics)에서 표본(sample)은 모집단(population)에서 추출한 데이터 집합을 의미합니다. 이는 모집단의 특성을 추정하기 위해 선택된 여러 개의 관측값으로 구성됩니다. 예를 들어, 한 도시의 전체 주민을 모집단이라고 할 때, 그중에서 500명을 무작위로 추출한 데이터 집합이 통계적 의미의 표본입니다. 통계학에서의 표본은 모집단의 특성을 파악하기 위한 모집단의 부분집합을 나타내는 용어로 사용됩니다.

확률이론과 통계학에서의 표본의 비교

특징	확률이론에서의 표본	통계학에서의 표본
표본의 정의	표본 공간에서 선택된 단일 결과 또는 사건	모집단에서 선택된 여러 개체 또는 관측값의 집합
주요 목적	사건의 확률을 모델링하고 계산	모집단의 특성을 추정하거나 가설을 검정
표본의 수	주로 하나의 결과	여러 개의 관측값으로 구성
분야 내 위치	확률이론의 기본 개념 중 하나	통계학의 데이터 수집 및 분석의 핵심 요소
관련 개념	확률 분포, 사건, 확률 공간	표본 통계량, 추정, 가설 검정, 표본 추출 방법
표본 추출 방법	특정 추출 방법보다는 모든 가능성을 고려	무작위 표본추출, 층화 표본추출 등 다양한 방법 사용

Q-dataset : 2

Q&A : 23

Quiz : 180

0000-0000