확률이론에서 표본공간과 벡터공간을 연결하는 함수는?

양적 확률변수(quantitative random variable) 또는 양적 확률벡터(quantitative random vector)입니다.

확률변수 또는 확률벡터를 함수라고 하는 이유는 표본공간의 원소를 벡터공간의 점 또는 점의 집합으로 변환하는 기능을 하기 때문입니다.

확률변수를 기호로 표현하면 다음과 같습니다.

$$X : \Omega \to \mathbb{R}$$

여기서, $X$는 양적(수치형) 확률변수

$\Omega$는 표본공간

$\mathbb{R}$는 $1$차원 벡터공간

확률벡터를 기호로 표현하면 다음과 같습니다.

$$X : \Omega \to \mathbb{R}^k$$

여기서, $X$는 양적(수치형) 확률벡터

$\Omega$는 표본공간

$\mathbb{R}^n$는 $k$차원 벡터공간

확률이론에서 육면주사위에 숫자를 부여하는 행위는 확률변수인가?

육면주사위의 6면은 표본공간의 표본에 해당합니다. 각각의 6면에 숫자를 부여하는 행위가 확률론적 목적(확률 계산, 사건 정의)에 사용된다면, 이는 확률변수로 간주됩니다. 반면, 단순히 라벨링 목적으로 숫자를 부여한다면, 이는 확률변수로 보지 않습니다.

Table 1. 확률이론에서 확률변수와 라벨링 비교

특성	확률변수	라벨링
목적	확률 계산 및 사건 정의에 사용	단순히 식별하기 위해 숫자를 부여
수학적 정의	함수: $( X : \Omega \to \mathbb{R} )$.	–
예제	$ P(X \leq 3) = P(\{1, 2, 3\}) $.	주사위 면에 1, 2, …, 6을 라벨링
연속형 변수로 확장	확장 가능	확장 불가

확률이론에서 확률변수의 역할은?

확률변수는 확률이론의 핵심 도구로, 추상적인 표본공간을 수치화하여 사건 정의, 확률 계산, 확률분포 분석, 기댓값 및 분산 계산, 데이터분석 등 다양한 역할을 수행합니다. 이러한 역할 덕분에 확률변수는 머신러닝 등 실질적인 응용에서도 필수적인 개념입니다.

Table 2. 확률변수의 역할

역할	설명
표본공간의 수치화	표본 공간의 원소를 수치(스칼라 또는 벡터)로 변환
사건정의 간소화	사건을 간단하고 체계적으로 표현 가능
확률분포 정의	누적 분포 함수(CDF)와 확률 밀도 함수(PDF)를 정의
확률계산의 도구	$ P(X \in B) $와 같은 형태로 확률을 계산
확률적 특성 정의	기댓값, 분산, 공분산 등 확률적 특성을 정의
다변량 데이터 분석	다변량 확률 변수로 변수 간 관계 분석 및 모델링 가능
데이터분석과 응용	머신러닝 등 다양한 응용 분야에서 활용

연속 표본공간으로 구성된 확률공간에서 확률변수의 역할은?

연속 표본공간으로 구성된 확률공간에서 확률변수는 표본공간의 원소를 실수값(또는 벡터값)으로 매핑하고, 이를 통해 사건정의, 확률분포, 확률계산을 체계적으로 수행할 수 있게 합니다.

연속 표본공간의 구조를 변환할 수 있게 함

표본공간이 연속적인 수치 구간일 때, 그 원소를 그대로 사용할 수도 있지만, 확률변수를 통해 원소를 변환하는 경우가 많습니다. 이때 사건정의나 확률계산이 확률변수를 기준으로 이루어집니다.

확률변수가 표본공간의 원소를 제곱하여 새로운 값을 매핑하는 예

표본공간: $\Omega=[0, 1]$
확률변수: $X(\omega)=\omega^2$

사건을 정의하는 도구

확률변수는 사건을 간단하게 표현할 수 있게 합니다.

연속 표본공간에서 구간으로 표현된 사건의 예

표본공간: $\Omega=[0,1]$
확률변수: $X(\omega)=\omega^2$
사건: $A=\{\omega\in \Omega \mid \omega^2 \leq 0.5\} \rightarrow X\leq0.5$

사건공간 생성

확률변수는 연속 확률공간에서 사건공간(시그마 대수)을 생성하는 역할을 합니다.
확률변수를 통해 정의된 사건공간은 다음과 같이 표현됩니다

$$\sigma(X) = \{X^{-1}(B) \mid B \in \mathcal{B}(\mathbb{R})\}$$

여기서, $\sigma(X)$은 확률변수($X$) 가 생성하는 사건공간:

확률변수, $X$와 관련된 사건들의 시그마대수($\sigma$-algebra)

$X^{-1}(B)$은 표본공간($\Omega$)에서 $X(\omega)$가 $B$라는 집합에 매핑되는 원소($\omega$)들의 집합:

$X^{-1}(B)=\{\omega\in \Omega \mid X(\omega) \in B \}$

$\mathcal{B}(\mathbb{R})$은 실수집합$(\mathbb{R})$에서의 보렐 시그마대수

예를 들어, 다음과 같은 조건에서

표본공간: $\Omega=[0,1]$
확률변수: $X(\omega)=\omega^2$
$B=[0, 0.25]$

다음식이 성립합니다.

$$X^{-1}(B)=\{\omega \in \Omega \mid \omega^2 \in [0, 0.25]\}=[0,0.5]$$

다차원적 분석을 가능하게 함

표본공간이 단일 연속구간이더라도 확률변수는 이를 벡터공간으로 확장할 수 있습니다.

단일연속구간 $\Omega=[0.1]$의 ($X_1, X_2$)의 2차원 벡터로의 확장의 예

확률변수: $X_1(\omega)=\omega$, $X_2(\omega)=\omega^2$

확률분포를 정의

표본공간 자체에는 확률이 정의되지 않으며, 사건에 대해 확률을 정의해야 합니다. 확률변수는 사건을 정의하고, 확률 분포(CDF, PDF)를 계산할 수 있도록 돕습니다.

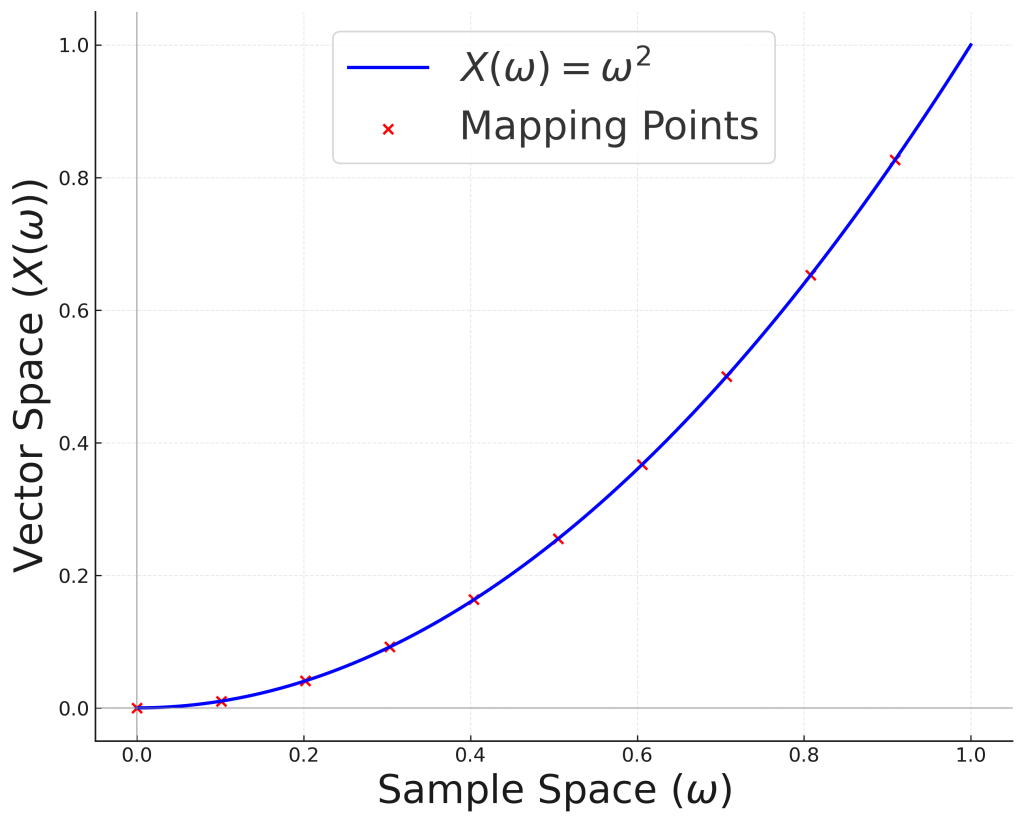
Fig. 1. 표본공간과 벡터공간을 연결하는 함수인 확률변수

Q-data : 2

Q&A : 23

Quiz : 180

0000-0000