네, 연쇄법칙에 따라 n개의 조건부확률분포의 곱으로 분해할 수 있습니다.
$n$개의 확률변수 $X_1, X_2, \cdots, X_n$의 결합확률분포는 $n$개의 조건부확률분포의 곱으로 분해할 수 있습니다.
$$
P(X_1, X_2, \dots, X_n)
\;=\;
P(X_1 \mid \varnothing)\, P(X_2 \mid X_1)\, P(X_3 \mid X_1, X_2)\, \cdots \, P(X_n \mid X_1, \dots, X_{n-1})
$$
여기서, $P(X_1 \mid \varnothing)$는 조건이 없는 $X_1$의 확률분포, 즉, 주변확률분포: $P(X_1 \mid \varnothing)=P(X_1)$
결합확률 $P(X_1, X_2, \dots, X_n)$은 확률변수의 실현 순서와 무관하며 조건부확률은 확률변수의 실현 순서에 따라 다릅니다.
연쇄법칙으로 표현된 n개의 확률분포의 결합확률분포의 첫번째 조건부확률분포는 주변분포이므로 1개의 주변확률분포와 (n-1)개의 조건부확률분포의 곱으로 분해된다고도 할 수 있습니다.
$$P(X_1, \cdots, X_n)=P(X_1)\prod_{i=2}^{n}P(X_i\mid X_i, \cdots, X_{i-1})$$
n개의 연속확률분포의 결합확률분포는 1개의 주변확률분포와 무한개의 조건부확률분포의 집합입니다.
확률변수가 모두 서로 독립인 경우, n개의 확률분포의 결합확률분포는 그 n개의 확률분포의 곱으로 분해됩니다.
$$
P(X_1, X_2, \dots, X_n)
\;=\;
P(X_1)\, P(X_2)\, P(X_3)\, \cdots \, P(X_n)
$$
결합확률분포(joint probability distribution)를 결합분포(join distribution), 공동확률분포, 공동분포라고 부르기도 합니다.
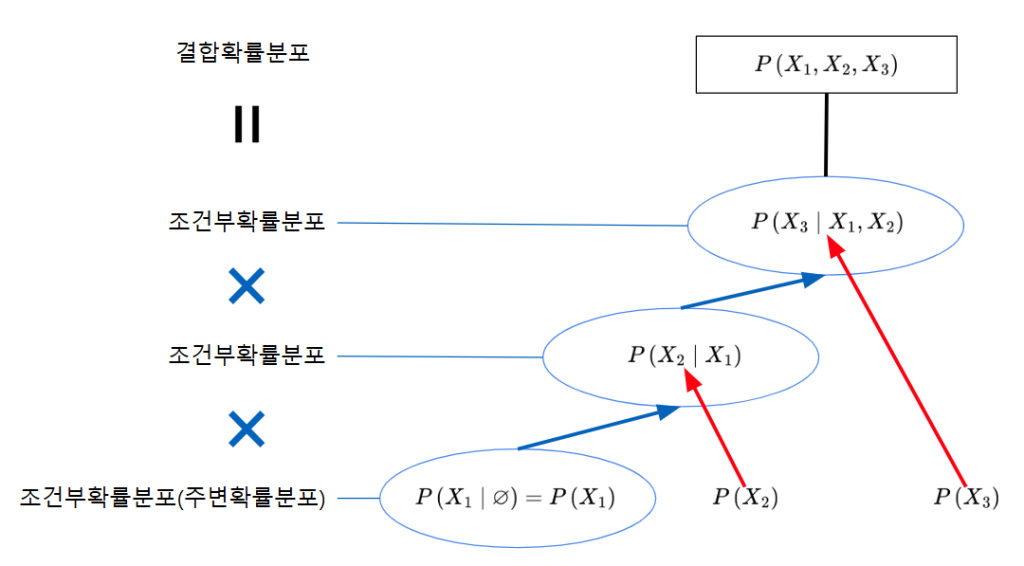
Fig1. 결합확률분포의 트리
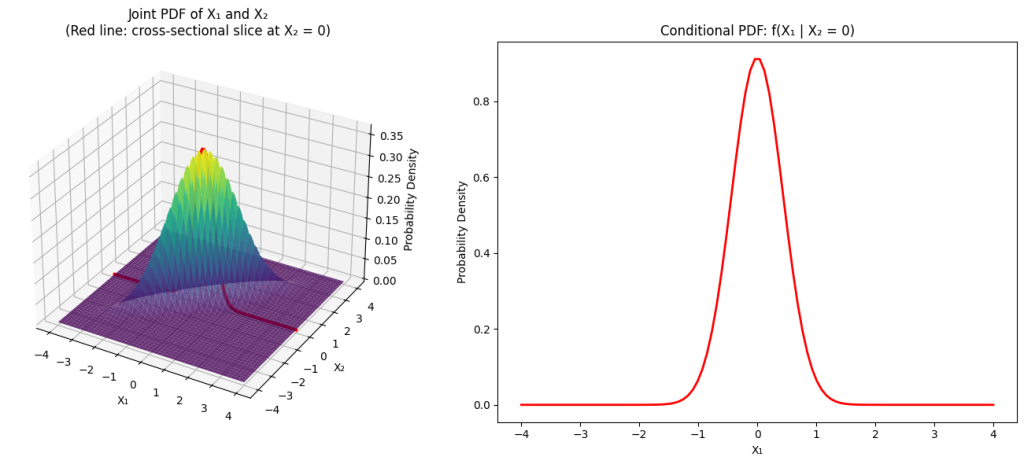
Fig2. 독립이 아닌 두 확률분포의 결합확률분포, 주변확률분포값과 우도의 곱이 이루는 단면분포(조건부분포)
Table1. 결합확률분포와 단면분포의 생성
| 항목 | 값 | 설명 |
|---|---|---|
| $\mu_1$ | 0 | $X_1$의 평균 |
| $\mu_2$ | 0 | $X_2$의 평균 |
| $\sigma_1$ | 1 | $X_1$의 표준편차 |
| $\sigma_2$ | 1 | $X_2$의 표준편차 |
| $\rho$ | 0.9 | $X_1$과 $X_2$ 사이의 상관계수 |
| 단면을 만드는 조건 | $X_2 = 0$ | 조건부 확률분포 $P(X_1 \mid X_2=0)$ |
| 기울기 ($X_1$ on $X_2$) | 0.9 | E[$X_1$|$X_2=x$] = 0.9x, X2가 주어졌을 때 X1의 회귀선 기울기 |
| 절편 ($X_1$ on $X_2$) | 0 | E[$X_1$|$X_2=x$] = 0.9$x$+0, X2가 주어졌을 때 $X_1$의 회귀선 절편 |
두 개의 확률분포의 결합확률분포를 두 개의 조건부확률분포로의 분해를 다음식으로 표현할 수 있습니다.
$$
P(X_1, X_2)
\;=\;
P(X_1 \mid \varnothing)\, P(X_2 \mid X_1)=P(X_2 \mid \varnothing)\, P(X_1 \mid X_2)
$$
여기서, $P(X_1, X_2)$는 $X_1$과 $X_2$가 동시에 특정값을 가지는 사건의 확률
여기서, $P(X_1 \mid \varnothing)$는 조건이 없는 $X_1$의 확률분, 즉, 주변확률분포: $P(X_1 \mid \varnothing=P(X_1)$
$P(X_1 \mid X_2)$는 $X_2$가 특정값으로 실현되었을 때 $X_1$가 특정값으로 실현되는 확률
$P(X_2 \mid X_1)$는 $X_1$가 특정값으로 실현되었을 때 $X_2$가 특정값으로 실현되는 확률
$P(X_1, X_2)$는 $X_1$와 $X_2$의 실현 순서와 무관하며 조건부확률은 실현 순서와 유관하여 $P(X_1\mid X_2)$와 $P(X_2\mid X_1)$로 다르게 표현합니다.
확률변수가 모두 서로 독립인 경우의 결합확률분포는 다음식과 같이 각 확률분포의 값의 곱으로 표현됩니다.
$$
P(X_1, X_2, \dots, X_n)
\;=\;
P(X_1)\, P(X_2)\, P(X_3)\, \cdots \, P(X_n)
$$
연쇄법칙(chain rule)은 확률론에서 여러 확률변수의 결합확률분포를 각 변수에 대한 조건부확률의 곱으로 분해하는 중요한 성질입니다.
예를 들어, 두 확률변수 $X_1$와 $X_2$에 대해, 조건부 확률의 정의에 따라 두 확률변수의 결합확률분포를 다음식과 같이 표현할 수 있습니다.
$$
P(X, Y) = P(X) \, P(Y \mid X) = P(Y) \, P(X \mid Y)
$$
일반적으로 연쇄법칙에 의한 $n$개의 확률변수 $X_1, X_2, \dots, X_n$의 결합확률분포는 다음과 같이 분해됩니다.
$$
P(X_1, X_2, \dots, X_n)
\;=\;
P(X_1) \, P(X_2 \mid X_1) \, P(X_3 \mid X_1, X_2) \, \cdots \, P(X_n \mid X_1, \dots, X_{n-1})
$$
윗 식은 다음과 같이 3단계를 거쳐 유도될 수 있습니다.
1. 먼저 두 변수에 대해 조건부확률의 정의를 적용하면,
$$P(X_1, X_2)=P(X_1)P(X_2\mid X_1)$$
2. 세 변수 $P(X_1, X_2, X_3)$의 경우, 결합확률분포는
$$
\begin{aligned}
P(X_1, X_2, X_3) &= P(X_1, X_2) \, P(X_3 \mid X_1, X_2) \\
&= P(X_1) \, P(X_2 \mid X_1) \, P(X_3 \mid X_1, X_2)
\end{aligned}
$$
3. 이 과정을 $n$개의 변수에 대해 반복하면 위의 일반적인 연쇄법칙을 얻을 수 있습니다.
$$P(X_1, \cdots, X_n)=P(X_1)\prod_{i=2}^{n}P(X_i\mid X_i, \cdots, X_{i-1})$$
연쇄법칙은 베이즈정리의 유도, 복잡한 확률모델을 구성하는 데 매우 유용합니다.
두 변수 $X_1$과 $X_2$에 대해 결합확률분포는 연쇄법칙을 이용해 다음과 같이 표현할 수 있습니다.
$$P(X_1, X_2)=P(X_2 \mid X_1)P(X_1)=P(X_1 \mid X_2)P(X_2)$$
윗 식에서, 베이즈정리는 결합확률분포의 두 표현을 서로 연결하는 관계를 나타냅니다. 구체적으로 $P(X_1\mid X_2)$를 구하고자 할 때 베이즈정리는 다음과 같이 유도됩니다.
1. 연쇄법칙에 따라
$$P(X_1, X_2)=P(X_2 \mid X_1)P(X_1)$$
2. 위 식을 $P(X_2)$로 나누면
$$\dfrac{P(X_1, X_2)}{P(X_2)}=\dfrac{P(X_2 \mid X_1)P(X_1)}{P(X_2)}$$
3. 좌변은 $P(X_1\mid X_2)$가 되므로
$$P(X_1 \mid X_2)=\dfrac{P(X_2 \mid X_1)P(X_1)}{P(X_2)}$$
즉, 베이즈정리는 두 확률변수 $X_1$과 $X_2$의 결합확률분포 $P(X_1, X_2)$를 두 개의 조건부확률분포 $P(X_1\mid X_2)$와 $P(X_1 \mid \varnothing)$ 또는 $P(X_2\mid X_1)$과 $P(X_2 \mid \varnothing)$로 분해한 후, 그 관계를 재배열하여 $P(X_1 \mid X_2)$ 또는 $P(X_2 \mid X_1)$를 구하는 식입니다.
$$P(X_1, X_2)=P(X_1\mid X_2)P(X_1 \mid \varnothing)=P(X_2\mid X_1)P(X_2 \mid \varnothing)$$