DATA SCIENCE : 27
DATA SCIENCE eISSN
a의 자연로그값, ln(a)입니다.
밑(base)이 $a$인 지수함수(exponential function), $f(x)=a^x$에서 $x=0$일 때의 변화율은 $\ln(a)$입니다. 변화율은 미분계수(derivative)입니다.
$$f'(0) = \lim_{h \to 0} \frac{f(0+h) – f(0)}{h}= \lim_{h \to 0} \frac{a^h – 1}{h}= \ln(a)$$
여기서, $f(0) = a^0 = 1$
$f(0+h) = a^h$
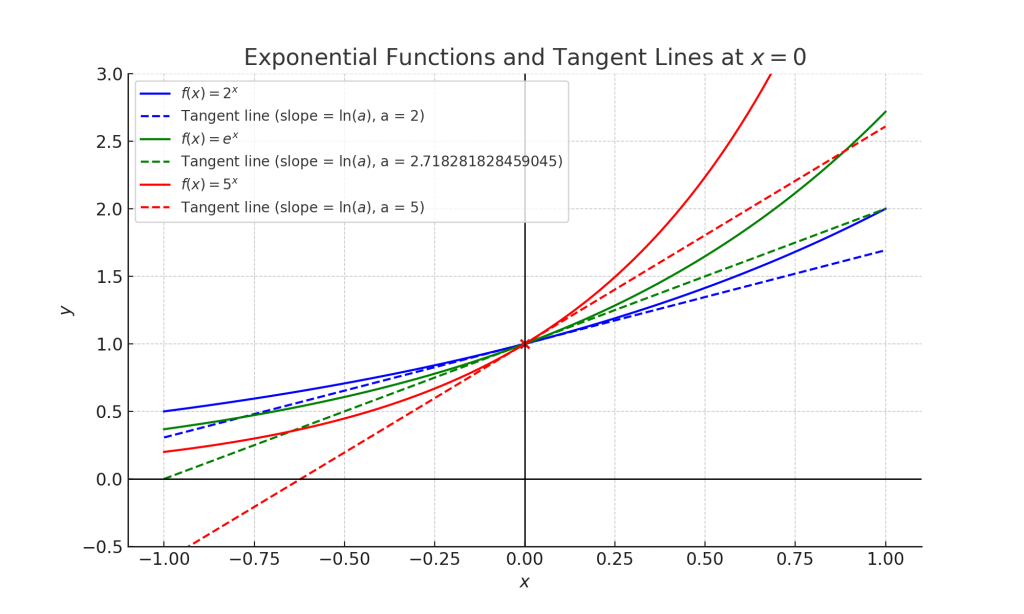
Fig.1 지수가 0이고, 밑이 2, e, 5일 때 변화율(접선의 기울기) 비교
지수함수 $f(x)=a^x$를 자연상수 e로 표현하면
$$a^x=e^{\ln(a^x)}=e^{x\ln{a}}$$
여기서, $a$는 양의 실수
$\ln(a^x)=x\ln(a)$
지수 함수 $f(x) = a^x $의 도함수를 자연상수 e 로 표현하면
원함수(원래 함수)
$$
f(x) = a^x
$$
원함수를 자연상수 e 를 이용하여 밑을 변환하면
\[
f(x) = a^x = e^{x \ln(a)}
\]
원함수를 미분하여 도함수를 구하면
\[
\frac{d}{dx} e^{x \ln(a)} = e^{x \ln(a)} \cdot \ln(a)
\]
따라서 도함수는
\[
f'(x) = a^x \ln(a)
\]
예) a = 2 일 때
$$f(x) = 2^x, \quad f'(x) = 2^x \ln(2)$$
예) a = e 일 때, e는 자연상수이며 약 2.71828…
\[
f(x) = e^x, \quad f'(x) = e^x \ln(e) = e^x \times 1 = e^x
\]
예) a = 5 일 때
\[
f(x) = 5^x, \quad f'(x) = 5^x \ln(5)
\]
지수함수에서 지수가 0일 때의 변화율을 자연로그로 표현
\[
\lim_{\Delta x \to 0} \frac{a^{\Delta x} – 1}{\Delta x}=\lim_{\Delta x \to 0} \frac{e^{\Delta x \ln(a)} – 1}{\Delta x} = \lim_{u \to 0} \frac{e^u – 1}{\frac{u}{\ln(a)}}= \lim_{u \to 0} \frac{e^u – 1}{u} \cdot \ln(a)= \ln(a)
\]
여기서, $a^{\Delta x} = e^{\Delta x \ln(a)}$
$u = \Delta x \ln(a)$
$\Delta x = \frac{u}{\ln(a)}$
$\lim\limits_{u \to 0} \frac{e^u – 1}{u} = 1$: 자연지수함수의 극한 성질
자연지수함수(natural exponential function)의 극한 성질의 유도
\[
\lim_{x \to 0} \frac{e^x – 1}{x} = \lim_{x \to 0} \frac{x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots}{x}= \lim_{x \to 0} \left( 1 + \frac{x}{2!} + \frac{x^2}{3!} + \cdots \right)= 1
\]
여기서, $e^x – 1 = x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$
$e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots$: 테일러급수
테일러 급수는 함수 $f(x)$를 점$a$ 근처에서 무한 다항식으로 표현하는 방법입니다. 특히, $a=0$ 일 때는 맥클로린 급수라고 부릅니다. 자연지수함수 $e^x$ 의 테일러 급수는 미적분학에서 가장 중요한 예 중 하나입니다.
테일러 급수 정의
\[
\boldsymbol{f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x – a)^n}
\]
\[
= f(a) + f'(a)(x – a) + \frac{f”(a)}{2!}(x – a)^2 + \frac{f^{(3)}(a)}{3!}(x – a)^3 + \cdots
\]
맥클로린 급수 (a = 0 인 경우)
\[
\boldsymbol{f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n}
\]
예) 자연지수 함수 $e^x$ 의 테일러 급수
\[
e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots
\]
테일러 급수의 활용
– 함수의 근사 계산: 복잡한 함수도 테일러 급수로 근사할 수 있습니다.
– 미분 방정식 풀이: 급수로 표현하면 해를 구하기 쉬운 경우가 있습니다.
– 정확한 함수 표현: 급수를 무한히 더하면 정확하게 원래 함수를 표현할 수 있습니다.
함수 $f(x)$를 어떤 점 $x=a$근처에서 다항식의 무한급수로 근사 표현
\[
f(x) \approx P_n(x) = C_0 + C_1(x – a) + C_2(x – a)^2 + \cdots + C_n(x – a)^n
\]
함수와 다항식의 값이 일치하도록 만들기
\[
f(a) = P_n(a) = C_0 \implies C_0 = f(a)
\]
1계 도함수의 일치
\[
f'(a) = P_n'(a) = C_1 \implies C_1 = f'(a)
\]
k계 도함수의 일치 (일반화)
\[
f^{(k)}(a) = P_n^{(k)}(a) \implies C_k = \frac{f^{(k)}(a)}{k!}
\]
테일러 급수 공식
\[
f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x – a)^n
\]
맥클로린 급수 (a = 0 인 경우)
\[
\boldsymbol{f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(0)}{n!}x^n}
\]