기울기의 제곱과 같아집니다.
오차가 거의 없어진다면, 종속변수 $Y$ 의 변동성은 거의 전적으로 독립변수 $X$에 의해 설명됩니다. 이때 분산의 비는 바로 기울기의 제곱과 같아집니다.
\[
\dfrac{\mathrm{Var}(Y)}{\mathrm{Var}(X)} \to \beta_1^2 \quad \text{as } \sigma^2 \to 0
\]
단순선형회귀에서 오차항의 표준편차가 작아지면 종속변수와 독립변수의 표준편차의 비는 기울기와 같아집니다.
\[
\frac{\mathrm{SD}(Y)}{\mathrm{SD}(X)} \to |\beta_1| \quad \text{as } \sigma \to 0
\]
단순선형회귀모델
\[
Y = \beta_0 + \beta_1 X + \epsilon, \quad \epsilon \sim N(0, \sigma^2)
\]
종속변수 $Y$의 분산
\[
\mathrm{Var}(Y) = \beta_1^2 \cdot \mathrm{Var}(X) + \sigma^2
\]
$X$의 분산이 커질수록 $Y$의 분산도 커집니다.
종속변수와 독립변수의 분산비
\[
\dfrac{\mathrm{Var}(Y)}{\mathrm{Var}(X)} = \beta_1^2 + \dfrac{\sigma^2}{\mathrm{Var}(X)}
\]
오차의 분산이 0으로 수렴하며 작아지면
\[
\sigma^2 \to 0 \quad \Rightarrow \quad \frac{\mathrm{Var}(Y)}{\mathrm{Var}(X)} \to \beta_1^2
\]
오차 분산이 작아질수록, 종속변수의 분산은 거의 독립변수에 의해 설명됩니다.
이때 종속변수의 분산은 $\beta^2\cdot \mathrm{Var}(X)$에 수렴하며 두 분산의 비는 기울기의 제곱으로 수렴합니다.
오차가 거의 없어진다면, 종속변수 $Y$ 의 변동성은 거의 전적으로 독립변수 $X$에 의해 설명됩니다. 이때 분산의 비는 바로 기울기의 제곱과 같아집니다.
\[
\dfrac{\mathrm{Var}(Y)}{\mathrm{Var}(X)} \to \beta_1^2 \quad \text{as } \sigma^2 \to 0
\]
단순선형회귀에서 오차항의 표준편차가 작아지면 종속변수와 독립변수의 표준편차의 비는 기울기와 같아집니다.
\[
\frac{\mathrm{SD}(Y)}{\mathrm{SD}(X)} \to |\beta_1| \quad \text{as } \sigma \to 0
\]
분산분해
\[
\text{전체분산} = \text{설명된 분산} +\text{설명되지 않은 분산}
\]
단순선형회귀모델의 분산분해 식
\[
\mathrm{Var}(Y) = \beta_1^2 \cdot \mathrm{Var}(X) + \sigma^2
\]
여기서, $\sigma^2$은 오차분산이며 설명되지 않은 분산
결정계수($R^2$)
$$R^2=\dfrac{\text{설명된 분산}}{\text{전체분산}}$$
결정계수 $R^2$은 0과 1사이의 값입니다.
따라서 결정계수의 여비율은 설명되지 않은 분산과 전체분산의 비입다.
$$1-R^2=\dfrac{\text{설명되지 않은 분산}}{\text{전체분산}}$$
단순선형회귀모델의 결정계수
\[
R^2 = \frac{\beta_1^2 \cdot \mathrm{Var}(X)}{\mathrm{Var}(Y)} \quad \Rightarrow \quad \mathrm{Var}(Y) = \frac{\beta_1^2 \cdot \mathrm{Var}(X)}{R^2}
\]
따라서
\[
\dfrac{\mathrm{Var}(Y)}{\mathrm{Var}(X)} = \dfrac{\beta_1^2}{R^2}
\]
단순선형회귀모델에서 설명되지 않은 분산과 전체분산의 비율은 오차분산과 종속변수의 분산의 비율입니다. 이 비율은 회귀모델이 설명하지 못하는 변동의 비율입니다.
단순선형회귀모델에서의 회귀계수(기울기)
\[
\beta_1^2 = R^2 \cdot \dfrac{\mathrm{Var}(Y)}{\mathrm{Var}(X)}
\]
$R^2$이 고정되어 있을 때 $\beta_1^2$은 $Y$와 $X$의 분산의 비로 조정됩니다.
단순선형회귀모델의 분산분해식
$$\mathrm{Var}(Y)=\beta_1^2\cdot \mathrm{Var}(X)+\sigma^2$$
위식을 표준편차로 표현하면
\[
\mathrm{SD}(Y)^2 = (\beta_1 \cdot \mathrm{SD}(X))^2 + \sigma^2
\]
여기서, $\mathrm{SD}(Y)$은 종속변수의 표준편차이며 종속변수의 변동성을 표현
$\beta_1\cdot \mathrm{SD}(X)$는 설명변수 $X$로 설명이 가능한 변동성을 표현
$\sigma$는 오차항의 표준편차이며 설명이 불가능한 변동성을 표현
전체 표준편차인 종속변수 $Y$의 표준편차를 고정하면 Fig 1.과 같이 변동성을 반원으로 표현할 수 있습니다.
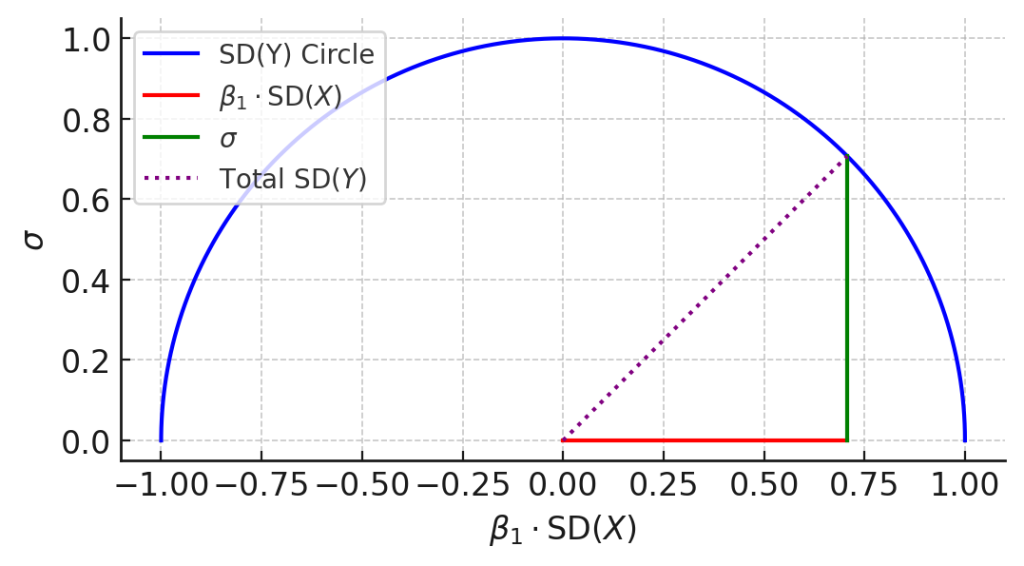
Fig.1 단순선형회귀모델의 변동성