두 확률변수가 독립이면, 해당 변수의 모든 사건이 독립적이라는 의미입니다.
두 변수의 결합확률분포(joint probability distribution)가 각 변수의 주위확률분포(marginal probability distribution)의 곱으로 표현됩니다.
질적데이터는 수치가 아닌 기호로 표현된 데이터입니다. 질적데이터는 명목척도와 순서척도로 구한 데이터입니다. 양적데이터는 수치로 표현된 데이터입니다. 양적데이터는 간격척도와 비례척도로 구한 데이터입니다.
모든 사건이 독립적
특정 조건 하에서만 독립, 제 3사건 하에서 독립
선형적 관계 존재
독립이 아닌 모든 경우
하나의 사건이 다른 사건을 완전히 결정
하나의 사건이 다른 사건의 원인
공통된 숨은 변수가 존재, 두 사건이 제 3의 사건에 의해 연결
일방적 인과 관계
데이터는 변수(변수명과 변수값)을 관측한 결과입니다. 데이터는 개체나 범주의 속성을 표현한 양적데이터와 질적데이터가 있으며 범주의 속성인 범주에 속하는 개체의 도수(빈도수, frequency)를 표현한 도수데이터가 있습니다.
Fig 1. 질적/양적데이터와 도수데이터 비교
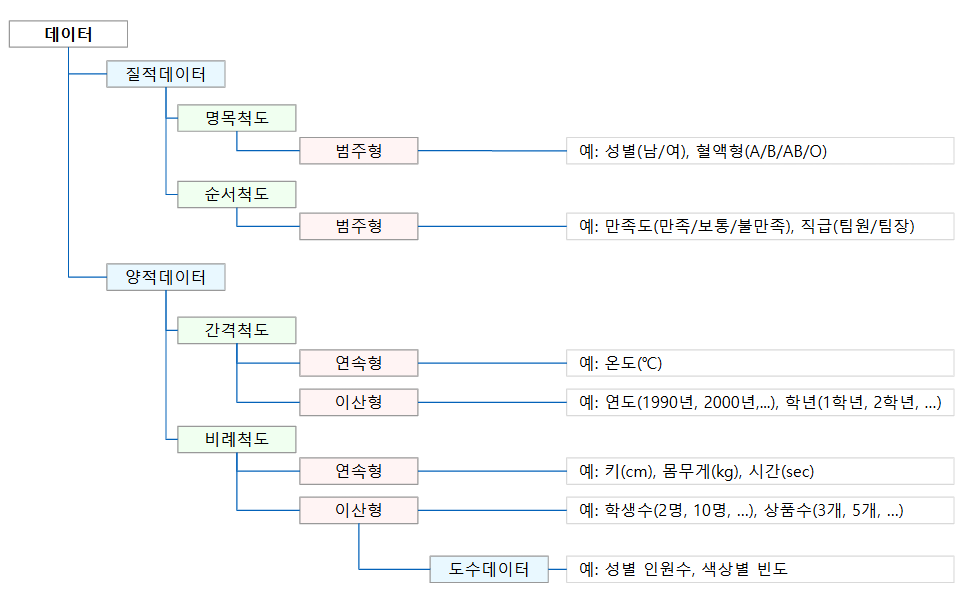
Table 1. 질적/양적데이터와 도수데이터 비교
| 데이터종류 | 척도 | 관측대상 | 관측값 의미 | 관측대상의 속성 형태 | 관측대상 – 관측대상의 속성 예시 | 관측값 예시 |
|---|---|---|---|---|---|---|
질적데이터 (qualitative) | 명목척도 (nominal scale) | 범주 (category) | 명목 | 범주형 (nominal) | 회사 – 산업분류 사람 – 성별 | { 전자, 전기, 화공, 기계, 식품 } { 남, 여 } |
개체 (indivisual) | 명목 | 범주형 | 대한민국 국민 – 주민번호 신청자 – ID | { 210427-XXXXXXX, … } { ID-1, … , ID-100 } | ||
순서척도 (ordinal scale) | 범주 | 순서 | 순서가 있는 범주형 | 음식점 – 서비스질 의류 – 크기 응시자 – 석차등급 | { 상, 중, 하 } { XS, S, M, L, XL } { 1 등급, … , 5등급} | |
| 개체 | 순서 | 순서가 있는 범주형 | 개인용 컴퓨터 – Serial Number | { 001, 002, … , 200 } | ||
양적데이터 (quantitative) | 간격척도 (interval scale) | 범주 | 위치 | 연속형 (continuous) | 국가 – 시간대 | { 1 동경시간대, … , 12 서경시간대 } |
| 개체 | 위치 | 연속형 | 사람 – 수명 | { y ; 0년 < y < 135년 } | ||
비례척도 (ratio scale) | 범주 | 크기 | 연속형 | 한국인 – 기대수명 | { y ; 55.3세 < y < 86.5세 } | |
| 개체 | 크기 | 연속형 | 사람 – 키 딸기 – 당도 | { y ; y > 100 cm } { y ; 0 Brix < y < 100 Brix } | ||
도수데이터 (frequecy) | 빈도척도 (frequency scale) | 범주 | 도수 | 이산형 (discrete) | 공장 – 1일 불량품수 | { 1 개, … } |
상대빈도척도 (ratio scale) | 범주 | 상대도수 | 연속형 | 딸기 – 용액 100 g 당 설탕의 무게 대한민국 국민 – 고혈압 비율 | { y ; 0 g < y < 100 g } { P ; 0 % < p < 100 % } |
연속형데이터(continuous data)와 범주형데이터(categorical data)는 관측대상인 개체의 속성에 따라 구분됩니다. 연속형데이터와 범주형데이터는 관측대상이 개체이며 연속형과 범주형으로 표현되는 개체의 속성의 관측값입니다.
연속형데이터는 관측대상인 개체의 속성이 연속적인 위치나 크기를 가지고 있음을 의미합니다. 개체의 속성은 간격척도나 비례척도로 관측하며 관측결과(관측값, 데이터)는 수치로 나타납니다. 여기서, 관측대상은 크기(양) 외에도 크기의 변화율도 될 수 있습니다. 크기를 관측한 연속형데이터의 예로는 키, 몸무게, 시간, 혈압 등이 있고 크기의 변화율을 관측한 연속형데이터는 경제성장률 등이 있습니다. 여기서의 관측대상의 속성은 연속적인 수로 표현되므로 개체의 속성을 관측한 관측값을 연속형데이터라고 부를니다. 연속적인 속성을 관측하기 위해서는 구간(계급, bin, bucket)을 가지는 척도를 사용하는 데 두가지 척도가 있습니다. 간격의 정보가 있는 간격척도와 간격척도의 간격에 간격크기의 비의 정보를 더한 비례척도가 있습니다. 따라서 연속형데이터는 개체의 연속형 속성을 간격척도나 비례척도로 관측한 수치를 의미한다고 할 수 있습니다. 그리고 연속형데이터는 아날로그인 관측대상을 디지털(수치)로 바꾼 데이터라고도 말할 수 있습니다. 간격척도나 비례척도에서 척도의 구간(계급, bin, bucket)을 범주로 볼 수 있습니다. 따라서 연속형데이터는 범주의 위치정보를 수치로 표현한 범주형데이터라고도 볼 수 있습니다. 이 때의 예로는 “나이”, “시험점수” 등이 있습니다.
범주형데이터는 관측대상인 개체가 속하는 범주명을 의미합니다. 개체가 속하는 범주는 개체의 속성이기도 하므로 범주명인 범주형데이터는 개체의 속성을 수치가 아닌 기호나 설명으로 표현할 수 있습니다. 예로는 국적, 사는 곳 등이 있습니다. 범주형데이터는 순서를 표현하기도 하는데 한우의 품질등급 등이 있습니다.
관측대상이 개체이면 정형데이터로 분류되고 관측대상이 범주이면 비정형데이터로 분류됩니다.
정형데이터는 관측대상이 개체입니다. 정형데이터는 개체의 속성을 관측한 결과인 관측값입니다. 정형데이터는 스프레드시트(spread sheet)나 데이터베이스(database)로 표현할 수 있습니다. 정형데이터는 개체의 속성의 형태를 지정할 수 있습니다. 따라서 정형데이터(structured data)는 미리 정의된 형식이 있는 데이터를 의미하기도 합니다. 상용스프레드시트(구글시트, 엑셀 등)의 각 셀은 셀안에 들어가는 데이터의 형식을 지정할 수 있습니다. 스프레드시트에서 사용하는 형식에는 텍스트, 숫자, 날짜 등이 있습니다.
비정형데이터(unstructured data)는 범주를 표현한 데이터입니다. 비정형데이터의 관측대상은 글이나 그림과 같은 범주입니다. 비정형데이터는 관측대상보다는 생성물로 더 잘 설명될 수 있습니다.
원시데이터는 처음 수집한 데이터입니다.
가공데이터는 1개 또는 다수개의 원시데이터에서 선택과 분리를 한 데이터입니다. 그리고 원시데이터나 가공데이터를 가지고 연산하여 나온 데이터도 가공데이터로 볼 수 있습니다. 정리하자면 원시데이터들에서 많은 가공데이터가 만들어질 수 있습니다.
명목척도를 제외한 순서척도, 간격척도, 비례척도로 관측한 데이터는 순서나 위치나 크기를 표현하므로 순서에 따라 나열할 수 있습니다. 순서에 따라 데이터를 나열하는 방법에는 두 가지 방법이 있습니다. 하나는 위치나 크기가 작은 값부터 큰 값으로 나열하는 오름차순이고 다른 하나는 큰 값부터 작은 값으로 나열하는 내림차순입니다. 데이터를 집합으로 표현하면, 다음과 같이 $n$개의 데이터를 순서가 낮은 값부터 표현합니다. 여기서, $x$는 데이터(변수값)를 의미하고 아랫첨자는 순서를 의미합니다.
$$x_{1}, x_{2}, \cdots , x_{n}$$
여기서, $x_{1} \lt x_{2} \lt \cdots \lt x_{n}$
최대값($x_{max}$)은 오름차순으로 나열한 집합의 원소에서 맨 우측의 값입니다.
$$x_{max} = x_{n}$$
최소값($x_{min}$)은 오름차순으로 나열한 집합의 순서에서 맨 좌측의 값입니다.
$$x_{min} = x_{1}$$
범위(range, $R$)는 최대값과 최소값의 차이입니다.
$$R=x_{max}-x_{min}$$
분위는 개체가 같은 도수를 가지는 범주입니다. 다시 말하면 같은 확률을 가지는 범주입니다. 분위수는 그 범주의 대표값입니다. 분위수는 간격척도로 구한 데이터는 중앙값으로 비례척도로 구한 데이터는 평균으로 표현됩니다. 간격척도, 비례척도로 구한 데이터의 분포는 분위와 분위수로 표현할 수 있습니다. 간격척도로 구한 데이터의 분위수는 중앙값으로 표현하며 비례척도로 구한 데이터의 분위수는 평균으로 표현합니다. 순서척도로 구한 데이터에서는 순서가 있는 범주가 다른 도수를 가지는 범주라고 할 수 있습니다. 여기서, 순서를 가지는 범주가 같은 도수를 가지면 분위와 분위수로 표현할 수 있습니다.
분위와 분위수의 응용에는 비례척도로 구한 데이터가 정규분포를 나타내는 지 살펴보는 Q-Q plot이 있습니다. Q-Q plot은 데이터로 부터 추정한 모수를 가지는 정규분포의 분위수를 X축으로 하고 개체의 관측값을 Y축으로 하는 좌표계에서 개체를 점으로 표현한 데이터시각화 방법니다. 그리고 개체 속성의 실제 데이터를 표현하는 Y축에서는 중앙값을 Y축의 원점좌표로 하고 X축에서는 정규분포를 표준정규분포로 표준화하여 0을 X축의 원점좌표로 정합니다. Q-Q plot에서는 X축을 표준정규분포로 표준화하여 개체가 나타내는 점들을 선형식으로 모델링하여 표준편차를 기준으로 하는 정규분포 구간을 관측하기도 합니다. Q-Q plot은 비례척도로 관측한 데이터가 정규분포를 나타내는 지 알기 위한 데이터시각화 방법입니다. 간격척도로 구한 데이터가 등간격을 나타낸다면 그 간격척도는 비례척도라고 할 수 있습니다. 또한 간격척도로 구한 데이터가 정규분포를 나타내기 위한 각 구간의 간격의 크기를 정하기 위한 직관을 제공합니다.
백분위수(percentile)는 관측대상의 속성을 표현하는 변수가 정의된 영역(정의역)에서 100개의 분위가 있을 때 각 분위에서의 대표값을 의미합니다. 여기서, 분위는 같은 데이터 개수를 가지는 순서가 있는 범주입니다. 분위수는 변수를 특정한 확률변수로 모델링하여 확률분포를 알 때 데이터세트를 통해 추정할 수 있으며 추정하는 방법에는 2가지가있습니다. 간격척도로 관측한 경우에는 최대값과 최소값을 분포함수와 데이터개수가 많은 데이터세트에서는 100등분하여 100개의 간격이 같은 구간인 분위(순서가 있는 범주) 만들고 각 구간의 평균을 그 구간의 데이터를 순서에 따라 나열하고 데이터의 개수를 100등분하여 데이터를 구분하였을 때 각 등분을 나눈 위치값입니다.
사분위수(quartile)는 quarter와 percentile의 합성어입니다. 간격척도나 비례척도로 구한 데이터는 위치 순으로 나열할 수 있습니다. 데이터를 오름차순으로 나얼한 후에 데이터를 같은 개수로 4등분하여 나눕니다. 이를 4개의 분위를 만든다고 할 수 있으며 분위는 순서를 가지는 범주라고 표현할 수 있습니다. 분위수는 각 분위의 위치값을 의미합니다. 특히 사분위수는 각 분위의 최대값을 의미합니다. 따라서 사(4)분위인 경우 1사분위, 2사분위, 3사분위의 위치값인 1, 2, 3사분위수는 데이터세트의 분포를 표현할 수있습니다. 그리고 2사분위수는 중앙값을, 4분위수는 데이터세트의 범위의 최대값을 의미합니다.
– 1사분위수(Q1)는 자신보다 작은 데이터가 전체의 25%
– 2사분위수(Q2)는 자신보다 작은 데이터가 전체의 50%
– 3사분위수(Q3)는 자신보다 작은 데이터가 전체의 75%
사(4)분위수와 백(100)분위수와의 관계
– 1사분위수 = 25백분위수
– 2사분위수 = 50백분위수
– 3사분위수 = 75백분위수
데이터는 질적 또는 양적 변수값의 집합입니다. 데이터와 정보 또는 지식은 종종 같은 의미로 사용하지만 데이터를 분석하면 정보가 된다고 볼 수 있습니다. 데이터는 일반적으로 연구의 결과물로 얻어집니다. 한편, 데이터는 경제(매출, 수익, 주가 등), 정부(예 : 범죄율, 실업률, 문맹율)와 비정부기구(예 : 노숙자 인구 조사)등 다양한 분야에서도 나타납니다. 그리고 데이터를 수집 및 분석하고 시각화할 수 있습니다.
일반적인 개념의 데이터는 응용이나 처리에 적합한 형태로 표현되거나 코딩됩니다. 원시 데이터 (“정리되지 않은 데이터”)는 “정리”되기 전의 숫자 또는 문자의 모음입니다. 따라서 데이터의 오류를 제거하려면 원시 데이터에서 데이터를 수정해야 합니다. 데이터 정리는 일반적으로 단계별로 이루어지며 한 단계의 “정리 된 데이터”는 다음 단계의 “원시 데이터”가 됩니다. 현장 데이터는 자연적인 “현장”에서 수집되는 원시 데이터입니다. 실험 데이터는 관찰 및 기록을 통한 과학적 조사에서 생성되는 데이터입니다. 데이터는 디지털 경제의 새로운 자원입니다.
데이터세트는 데이터의 집합입니다. 일반적으로 데이터세트는 단일 데이터베이스 테이블의 내용 또는 테이블의 모든 열이 특정 변수를 나타내는 단일 통계 데이터 행렬에 해당하며 각 행은 해당 데이터 집합의 특정 구성요소에 해당합니다. 데이터세트에는 각 개체의 변수값이 나열됩니다. 각 변수값을 데이텀이라고 합니다. 데이터세트는 행의 수에 대응하는 하나 이상의 개체(member)에 대한 데이터를 포함합니다. 데이터세트라는 용어는 특정 실험이나 이벤트에 해당하는 데이터를 적용하기 위해 좀 더 광범위하게 사용될 수도 있습니다.
데이터세트 보다 덜 사용되는 이름은 데이터 자료 및 데이터 저장소입니다. 사용 예는 우주인이 우주 탐사선을 타고 실험을 수행하여 데이터세트를 수집하는 것입니다. 매우 큰 데이터세트는 일반적인 데이터 처리프로그램이 처리하기에 부적합한데 이를 빅 데이터라고 합니다. 공개 데이터 분야에서 데이터세트는 공공 데이터저장소에서 공개정보를 측정하는 단위입니다. European Open Data 포털은 50 만 개 이상의 데이터세트를 가지고 있습니다.