네, 유의수준이 먼저 정해지고 확률분포 정보를 더하여 임계값이 결정되므로 유의수준이 임계값을 정합니다.
유의수준(significance level)은 가설검정에서 귀무가설을 기각하는 기준이 되는 확률입니다. 일반적으로 $\alpha$로 표시됩니다. 선행연구에 의해 주어집니다. 유의수준은 임계값을 설정하는 데 사용됩니다.
임계값 (critical value)은 귀무가설이 참이여서 귀무가설을 채택하는 영역과 귀무가설이 거짓이어서 귀무가설을 기각하는 영역의 경계값입니다. 임계값은 유의수준과 검정통계량의 분포에 따라 결정됩니다. 검정통계량의 분포에는 Z분포, t분포, 카이제곱분포 등이 있습니다. 또한 양측검정이나 단측검정에 따라서도 임계값은 달라집니다. 예를 들어, 유의수준이 0.05이고 Z분포이고 양측검정에서는 임계값이 2개이며 $pm1.96$입니다.
예를 들어, 의학 연구에서 새로운 약물의 효과를 검증할 때 유의수준을 0.05로 설정한다면, 이는 연구자가 약물의 효과가 없는데도 효과가 있다고 잘못 결론내릴 확률을 5%로 제한하겠다는 의미입니다. 이는 환자 안전과 직결되므로 가장 먼저 결정하여야 할 값입니다.
유의수준은 귀무가설이 참이라는 전제를 바탕으로 설정됩니다. 유의수준은 1종 오류를 범할 수 있는 확률의 설정값과 같습니다. 예를 들어, 유의수준이 0.05이라는 것은 귀무가설이 참이라는 전제 하에 데이터를 분석하였을 때 5%의 확률로 귀무가설을 잘못 기각할 수 있다라는 의미입니다.
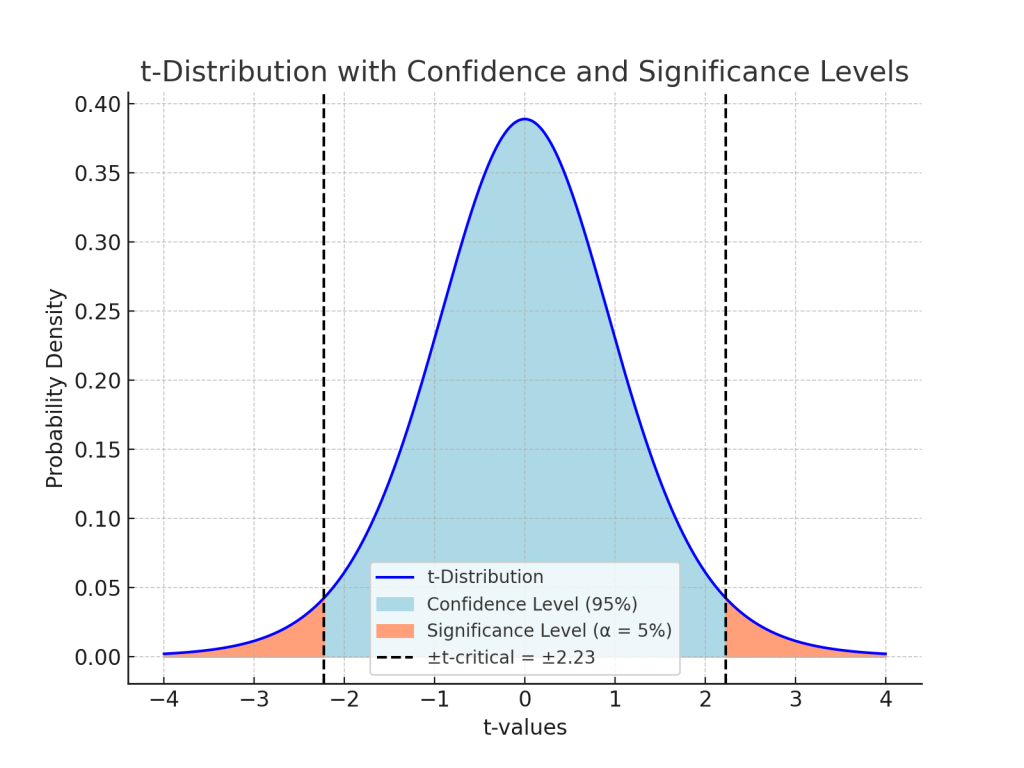
유의수준과 신뢰수준은 합해서 1이 되는 확률입니다. 즉, 배타적인 두 영역(범주)의 경계를 나타내는 비율입니다. 따라서 유의수준, 또는 신뢰수준에 의해 정해지는 임계값은 귀무가설이 참인 영역과 거짓인 영역의 경계를 의미합니다. 귀무가설에서의 “무(無)”의 위치는 귀무가설이 참인 영역에 있습니다.
Fig.1 의 푸른색이 귀무가설이 참인 신뢰수준의 영역이고 영역의 면적이 신뢰수준인 확률값입니다. 유의수준은 (1-신뢰수준)인 확률값입니다.
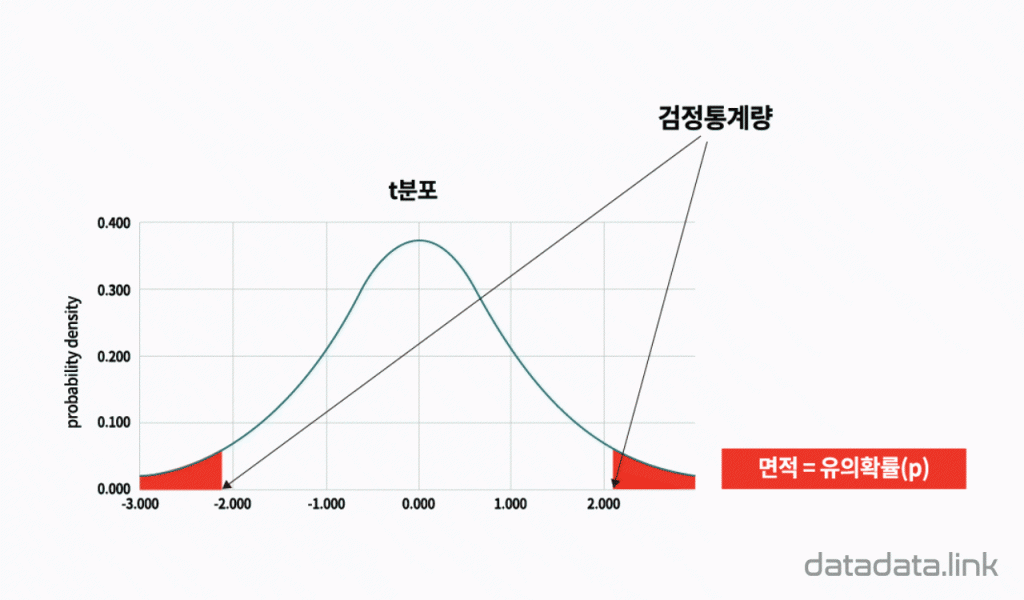
검정통계량이 유의확률을 정합니다. 확률변수값인 검정통계량이 확률인 유의확률(p값)을 정하게 됩니다. 이는 유의수준이 임계값을 정하는 것과 반대입니다. 유의수준은 연구자에 의해 주어지는 값이고 검정통계량은 수집한 데이터를 통해 얻은 값입니다. 가설을 검정하는 것은 유의수준과 검정통계량을 비교하는 것인 데 양을 비교하는 방법은 유의수준과 유의확률을 비교하는 것이고 위치를 비교하는 방법은 임계값과 검정통계량을 비교하는 것입니다. 귀무가설의 판정을 위해서는 위치보다는 양을 비교하는 것이 직관적입니다.