Menu
독립표본은 연속적인 관계를 가질 수 없습니다.
데이터셋은 표본이고 표본은 대응표본(paired samples)과 독립표본(independent samples)들로 이루어져 있다고 볼 수 있습니다. 표본은 개체들의 속성값의 모음입니다. 두 속성이 서로 대응되면 대응표본이고 두 속성이 서로 독립되면 독립표본이라고 합니다.
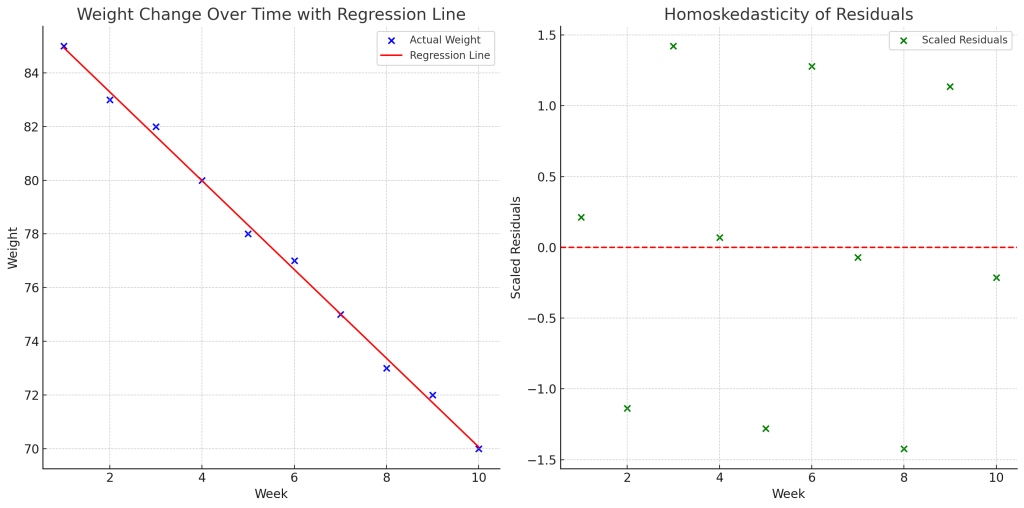
대응표본(paired samples)은 동일한 개체에서 반복적으로 측정될 수 있으므로 대응표본은 연속성이 있습니다. 즉 , 동일 개체가 대응되는 상태로 대응표본은 연속일 수 있습니다. 연속된 대응표본의 예로는 “운동 선수의 체력 테스트 결과를 매달 측정”, “다이어트 프로그램에 참여하는 사람의 체중을 매주 측정” 등이 있고 시간의 흐름에 따라 동일한 개체에서 반복적으로 측정된 데이터입니다. 연속된 대응표본을 분석하면 시간에 따른 변화를 보다 세밀하게 관찰하고 분석할 수 있습니다. 여기서, 중요한 점은 운동선수의 체력과 사람의 체중은 시간에 따라 적분되는 결과입니다.
각 독립표본의 데이터는 다른 독립표본의 데이터에 영향을 받지 않으며, 독립적으로 수집된 것입니다. 독립표본이 순차적으로 수집될 수는 있습니다. 실험 설계나 데이터 수집 방식에 따라 독립표본이 시간적 혹은 조건적으로 순차적으로 수집될 수는 있습니다. 예를 들어, 매일 다른 사람에게서 데이터를 수집하는 경우, 이러한 데이터는 독립표본이지만 시간적으로 순차적으로 수집된 것입니다. 하지만 이 경우에도 각 데이터 포인트는 여전히 다른 포인트와 독립적이어야 합니다.
단일표본(single sample)은 한 집단에서 수집된 데이터로, 이를 이용하여 특정한 통계적 가설을 검정하는 경우를 의미합니다. 단일표본 검정은 주로 모집단의 평균이나 비율이 특정 값과 다른지 여부를 판단하는 데 사용됩니다. 이 때 특정값은 주어집니다. 단일표본을 통한 가설검정의 예는 한 회사의 직원들의 평균 근무 시간이 주당 40시간인지 검정하는 것입니다. 이 때 단일표본의 크기가 30이상이면 Z분포를 쓸 수 있고, 표본크기에 따라 보다 정밀하게 본다면 t분포를 사용할 수 있습니다. 표본크기가 30일 때, Z분포와 t분포에서 동일하게 95% 신뢰구간을 구한다면, 그 차이는 약 0.09입니다.
네, 연속된 대응표본은 회귀 분석을 통해 표현할 수 있습니다. 연속된 대응표본 데이터를 사용하여 시간에 따른 변화나 트렌드를 분석하고 예측하기 위해 회귀 분석이 자주 사용됩니다. 특히, 시계열 데이터나 반복 측정 데이터를 다룰 때 회귀 분석이 유용합니다.
